算法思维

算法（Algorithm）是为了解决一个特定的问题而精心设计的一套数学模型以及在这套数学模型上的一系列操作步骤，这些操作步骤是将描述的输入数据逐步处理、转换，并最后得到一个确定的结果。当然，准确性是基本前提，时间和空间效率是衡量一个算法优劣的重要评估标准。算法通常在函数中使用控制结构来实现。

算法分类

算法是一个比较大的概念范畴，为便于理解，可以从算法思想，典型应用及与数据结构的关系，将算法分为三类：

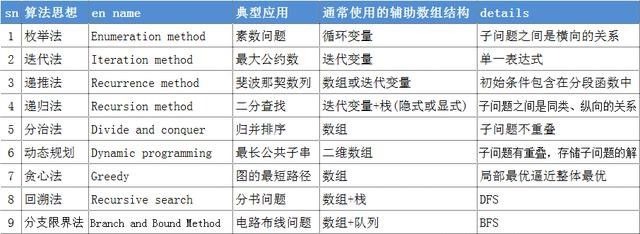
• 经典算法思想：一般来说，算法设计没有什么固定的方法可循。但是通过大量的实践，人们也总结出算法某些共性的规律，包括穷举法(Enumeration)、递推法(Recurrence)、递归法、分支法(Divide and Conquer)、贪心法、回溯法(Backtracking)、动态规划法等。
• 经典算法思想在典型问题上的应用：如排序、查找（检索）等算法。尽管计算学科的整个发展可以很短，但前人们还是留下了很多非常经典的算法，仅就排序而言，就可以数出一大堆，如冒泡排序法、快速排序法、选择排序法、插入排序法、基数排序法等。
• 在数据结构上应用的算法：包括增、查、删、改、遍历、图的最路径、最小生成树、树的遍历方法，线性表的二分查找，以及数据类型的运算符，类类型的操作符重载。有些算法充满着智慧，如Dijistra最短路径、Huffman树、蒙特卡洛方法、快速排序、堆排序、红黑树、A+树、字符串匹配的KMP算法等。

复杂的问题可以分而治之。对于复杂的问题，通常都需要应用分治的思想，同时，很多算法中也有分治思想的体现。分治法所能解决的问题一般具有以下几个特征：

• 该问题的规模缩小到一定的程度就可以容易地解决；
• 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质
• 利用该问题分解出的子问题的解可以合并为该问题的解；
• 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

因为问题的计算复杂性一般是随着问题规模的增加而增加，因此大部分问题满足这个特征。递归的子问题之间是同类、纵向的关系，而枚举是横向的关系。如果具备了前两条特征，而不具备第三条特征，则可以考虑贪心算法或动态规划。

特征4涉及到分治法的效率，如果各子问题是不独立的，则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然也可用分治法，但一般用动态规划较好。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，但是经分解得到的子问题往往不是互相独立的。不同子问题的数目常常只有多项式量级。在用分治法求解时，有些子问题被重复计算了许多次。如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，就可以避免大量重复计算，从而得到多项式时间算法。

递归算法求解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。这种性质称为子问题的重叠性质。动态规划算法，对每一个子问题只解一次，而后将其解保存在一个表格中，当再次需要解此子问题时，只是简单地用常数时间查看一下结果。通常不同的子问题个数随问题的大小呈多项式增长。因此用动态规划算法只需要多项式时间，从而获得较高的解题效率。

顾名思义，贪心算法总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑，它所作出的选择只是在某种意义上的局部最优选择。当然，希望贪心算法得到的最终结果也是整体最优的。虽然贪心算法不能对所有问题都得到整体最优解，但对许多问题它能产生整体最优解。如单源最短路径问题，最小生成树问题等。在一些情况下，即使贪心算法不能得到整体最优解，其最终结果却是最优解的很好近似。

贪心算法和动态规划算法都要求问题具有最优子结构性质，这是两类算法的一个共同点。严格地说，用动态规划的问题一般都有前后重叠的，需要用前一阶段的结果局部贪心推出下一个阶段结果。贪心算法一般要得到最优解只能各个阶段没有重叠，以局部最优构造全局最优。