堆排序
堆排序
堆排序 (Heapsort) 是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大顶堆和小顶堆,是完全二叉树。大顶堆的要求是每个节点的值都不大于其父节点的值,即 A[PARENT[i]] >= A[i]。在数组的升序排序中,需要使用的就是大顶堆,因为根据大顶堆的要求可知,最大的值一定在堆顶。那么依次把这个最大值交换到数组尾部,即可完成一个升序排列的过程。堆排序的一个优势在于可以只对某个较大的数组中的前 K 个进行排序,譬如从 N 个无序的整数中计算机最小的 K 个整数的算法,并给出时间复杂度,其中 K«N,要求时间复杂度尽可能的低,不要求 K 个整数排序。将 N 个数中的前 K 个建立一个小顶堆。每读入一个新的整数,就把它插入到堆中,调整堆,但是每次调整都只调整前 K 个元素。从第 K+1 个位置开始的元素都忽略。时间为 NlogK。
Complexity: 算法复杂度
稳定性
我们知道堆的结构是节点 i 的孩子为 2 _ i 和 2 _ i + 1 节点,大顶堆要求父节点大于等于其 2 个子节点,小顶堆要求父节点小于等于其 2 个子节点。在一个长为 n 的序列,堆排序的过程是从第 n / 2 开始和其子节点共 3 个值选择最大(大顶堆)或者最小(小顶堆),这 3 个元素之间的选择当然不会破坏稳定性。但当为 n / 2 - 1,n / 2 - 2,… 1 这些个父节点选择元素时,就会破坏稳定性。有可能第 n / 2 个父节点交换把后面一个元素交换过去了,而第 n / 2 - 1 个父节点把后面一个相同的元素没 有交换,那么这 2 个相同的元素之间的稳定性就被破坏了。所以,堆排序不是稳定的排序算法。
堆
堆(也叫优先队列),是一棵完全二叉树,它的特点是父节点的值大于(小于)两个子节点的值(分别称为大顶堆和小顶堆)。它常用于管理算法执行过程中的信息,应用场景包括堆排序,优先队列等。二叉堆是完全二叉树或者是近似完全二叉树。二叉堆满足二个特性:
- 父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
- 每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆:
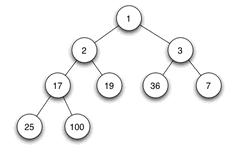
堆的存储上一般都用数组来表示堆,i 结点的父结点下标就为 (i – 1) / 2。它的左右子结点下标分别为 2 _ i + 1 和 2 _ i + 2。如第 0 个结点左右子结点下标分别为 1 和 2。

堆建立
操作主要是将数组 A 转化成一个大顶堆。思想是,先找到堆的最后一个非叶子节点(即为第 n/2 个节点),然后从该节点开始,从后往前逐个调整每个子树,使之称为堆,最终整个数组便是一个堆。子数组 A[(n/2)+1..n]中的元素都是树中 的叶子,因此都可以看作是只含有一个元素的堆。
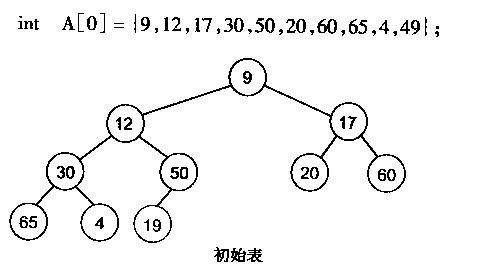
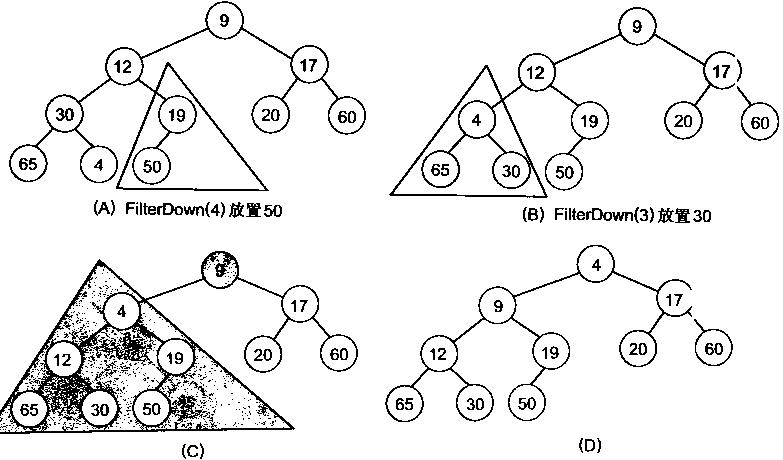
堆排序
“ 空间复杂度 ” 指占内存大小,堆排序每次只对一个元素操作,是就地排序,所用辅助空间 O(1),空间复杂度是 O(1 )
在构建堆的过程中,完全二叉树从最下层最右边的非终端结点开始构建,将它与其孩子进行比较和必要的互换,对于每个非终端结点来说,其实最多进行两次比较和互换操作,因此整个构建堆的时间复杂度为 O(n)。在正式排序时,第 i 次取堆顶记录重建堆需要用 O(logi) 的时间(完全二叉树的某个结点到根结点的距离为 ⌊log2i⌋+1),并且需要取 n-1 次堆顶记录,因此,重建堆的时间复杂度为 O(nlogn)。首先可以看到堆建好之后堆中第 0 个数据是堆中最小的数据。取出这个数据再执行下堆的删除操作。这样堆中第 0 个数据又是堆中最小的数据,重复上述步骤直至堆中只有一个数据时就直接取出这个数据。由于堆也是用数组模拟的,故堆化数组后,第一次将 A[0]与 A[n - 1]交换,再对 A[0…n-2]重新恢复堆。第二次将 A[0]与 A[n – 2]交换,再对 A[0…n - 3]重新恢复堆,重复这样的操作直到 A[0]与 A[1]交换。由于每次都是将最小的数据并入到后面的有序区间,故操作完成后整个数组就有序了。有点类似于直接选择排序。
完整的实例代码如下:
package wx.sorting.heap;
import wx.sorting.quick.QuickSort;
/**
* Created by apple on 16/4/23.
*/
public class HeapSort {
/**
* 堆筛选,除了start之外,start~end均满足大顶堆的定义。
* 调整之后start~end称为一个大顶堆。
*
* @param arr 待调整数组
* @param start 起始指针
* @param end 结束指针
*/
public static void heapAdjust(int[] arr, int start, int end) {
int temp = arr[start];
//这里需要重复交换是因为将父节点交换给子节点之后,子节点所处的堆可能就不是大顶堆了,所以需要递归的来调整
for (int i = 2 * start + 1; i <= end; i *= 2) {
//左右孩子的节点分别为2*i+1,2*i+2
//选择出左右孩子较大的下标
if (i < end && arr[i] < arr[i + 1]) {
i++;
}
if (temp >= arr[i]) {
break; //已经为大顶堆,=保持稳定性。
}
arr[start] = arr[i]; //将子节点上移
start = i; //下一轮筛选
}
arr[start] = temp; //插入正确的位置
}
/**
* @param arr
* @function 进行堆排序操作
*/
public static void heapSort(int[] arr) {
//首先根据输入的序列构造大顶堆,即把值最大的元素移到堆顶
//从第一个非子节点开始调整
//这里需要从子节点循环调用的原因是,只有到两个子节点所在的子堆已经是最大堆了,才能保证父节点与其子节点比较后就能保证把全局最大的元素替换上来
for (int i = arr.length / 2; i >= 0; i--) {
//这里调整当前非子节点与其子节点
heapAdjust(arr, i, arr.length - 1);
}
System.out.println("大顶堆为:");
for (int a : arr) {
System.out.print(a + " ");
}
//不断将堆顶值放入有序区,并且重复对无序区进行大顶堆修正
for (int i = arr.length - 1; i >= 0; i--) {
//把值最大的放到最后一个叶子节点处,即放入有序区中
swap(arr, 0, i);
//调整无序区的结构,使之成为大顶堆
heapAdjust(arr, 0, i - 1);
}
}
//交换左右的数
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String args[]) {
int[] arr = new int[]{3, 9, 7, 8, 5, 11, 32};
HeapSort.heapSort(arr);
System.out.println("排序后的数组为:");
for (int a : arr) {
System.out.print(a + " ");
}
}
/**
* 大顶堆为:
32 9 11 8 5 3 7
排序后的数组为:
3 5 7 8 9 11 32
*/
}
