递归法
递归法 Recursion method
递归,在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。简单来说,递归表现为函数调用函数本身,这样就把原问题的求解转换为许多性质相同但是规模更小的子问题。我们只需要关注如何把原问题划分成符合条件的子问题,而不需要去研究这个子问题是如何被解决的。递归和枚举的区别在于:枚举是横向地把问题划分,然后依次求解子问题,而递归是把问题逐级分解,是纵向的拆分。
递归最恰当的比喻,就是查词典。我们使用的词典,本身就是递归,为了解释一个词,需要使用更多的词。当你查一个词,发现这个词的解释中某个词仍然不懂,于是你开始查这第二个词,可惜,第二个词里仍然有不懂的词,于是查第三个词,这样查下去,直到有一个词的解释是你完全能看懂的,那么递归走到了尽头,然后你开始后退,逐个明白之前查过的每一个词,最终,你明白了最开始那个词的意思。
递归算法思想往往用函数的形式来体现,所以递归算法需要预先编写功能函数。这些函数是独立的功能,能够实现解决某个问题的具体功能,当需要时直接调用这个函数即可。在计算机编程应用中,递归算法对解决大多数问题是十分有效的,它能够使算法的描述变得简洁而且易于理解。递归算法有如下 3 个特点。
- 递归过程一般通过函数或子过程来实现。
- 递归算法在函数或子过程的内部,直接或者间接地调用自己的算法。
- 递归算法实际上是把问题转化为规模缩小了的同类问题的子问题,然后再递归调用函数或过程来表示问题的解。
递归代码最重要的两个特征:结束条件和自我调用,
- 自身调用:原问题可以分解为子问题,子问题和原问题的求解方法是一致的,即都是调用自身的同一个函数。
- 终止条件:递归必须有一个终止的条件,即不能无限循环地调用本身。
public int sum(int n) {
if (n <= 1) {
return 1;
}
return sum(n - 1) + n;
}
总结而言,在使用递归算法时,应该注意如下几点。
- 递归是在过程或函数中调用自身的过程。
- 在使用递归策略时,必须有一个明确的递归结束条件,这称为递归出口。
- 递归算法通常显得很简洁,但是运行效率较低,所以一般不提倡用递归算法设计程序。
- 在递归调用过程中,系统用栈来存储每一层的返回点和局部量。如果递归次数过多,则容易造成栈溢出,所以一般不提倡用递归算法设计程序。
递归解题思路
解决递归问题一般就三步曲,分别是:
- 第一步,定义函数功能
- 第二步,寻找递归终止条件
- 第二步,递推函数的等价关系式
定义函数功能
定义函数功能,就是说,你这个函数是干嘛的,做什么事情,换句话说,你要知道递归原问题是什么呀?比如你需要解决阶乘问题,定义的函数功能就是 n 的阶乘,如下:
// n的阶乘(n为大于0的自然数)
int factorial (int n){
}
寻找递归终止条件
递归的一个典型特征就是必须有一个终止的条件,即不能无限循环地调用本身。所以,用递归思路去解决问题的时候,就需要寻找递归终止条件是什么。比如阶乘问题,当 n=1 的时候,不用再往下递归了,可以跳出循环啦,n=1 就可以作为递归的终止条件,如下:
// n的阶乘(n为大于0的自然数)
int factorial (int n){
if(n==1){
return 1;
}
}
递推函数的等价关系式
递归的「本义」,就是原问题可以拆为同类且更容易解决的子问题,即「原问题和子问题都可以用同一个函数关系表示。递推函数的等价关系式,这个步骤就等价于寻找原问题与子问题的关系,如何用一个公式把这个函数表达清楚」。阶乘的公式就可以表示为 f(n) = n * f(n-1), 因此,阶乘的递归程序代码就可以写成这样,如下:
int factorial (int n){
if(n==1){
return 1;
}
return n * factorial(n-1);
}
递归的问题
- 递归调用层级太多,导致栈溢出问题
- 递归重复计算,导致效率低下
栈溢出问题
- 每一次函数调用在内存栈中分配空间,而每个进程的栈容量是有限的。
- 当递归调用的层级太多时,就会超出栈的容量,从而导致调用栈溢出。
- 其实,我们在前面小节也讨论了,递归过程类似于出栈入栈,如果递归次数过多,栈的深度就需要越深,最后栈容量真的不够咯
/
* 递归栈溢出测试
*/
public class RecursionTest {
public static void main(String[] args) {
sum(50000);
}
private static int sum(int n) {
if (n <= 1) {
return 1;
}
return sum(n - 1) + n;
}
}
Exception in thread "main" java.lang.StackOverflowError
at recursion.RecursionTest.sum(RecursionTest.java:13)
怎么解决这个栈溢出问题?首先需要「优化一下你的递归」,真的需要递归调用这么多次嘛?如果真的需要,先稍微「调大 JVM 的栈空间内存」,如果还是不行,那就需要弃用递归,「优化为其他方案」。
重复计算,导致程序效率低下
我们再来看一道经典的青蛙跳阶问题:一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
class Solution {
public int numWays(int n) {
if (n == 0){
return 1;
}
if(n <= 2){
return n;
}
return numWays(n-1) + numWays(n-2);
}
}
- 要计算原问题 f(10),就需要先计算出子问题 f(9) 和 f(8)
- 然后要计算 f(9),又要先算出子问题 f(8) 和 f(7),以此类推。
- 一直到 f(2) 和 f(1),递归树才终止。
我们先来看看这个递归的时间复杂度吧,「递归时间复杂度 = 解决一个子问题时间*子问题个数」
- 一个子问题时间 = f(n-1)+f(n-2),也就是一个加法的操作,所以复杂度是 「O(1)」;
- 问题个数 = 递归树节点的总数,递归树的总结点 = 2^n-1,所以是复杂度「O(2^n)」。
因此,青蛙跳阶,递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n),就是指数级别的,爆炸增长的,「如果 n 比较大的话,超时很正常的了」。回过头来,你仔细观察这颗递归树,你会发现存在「大量重复计算」,比如 f(8)被计算了两次,f(7)被重复计算了 3 次…所以这个递归算法低效的原因,就是存在大量的重复计算。既然存在大量重复计算,那么我们可以先把计算好的答案存下来,即造一个备忘录,等到下次需要的话,先去「备忘录」查一下,如果有,就直接取就好了,备忘录没有才再计算,那就可以省去重新重复计算的耗时啦!这就是「带备忘录的解法」。
一般使用一个数组或者一个哈希 map 充当这个「备忘录」。假设 f(10)求解加上「备忘录」,我们再来画一下递归树:「第一步」,f(10)= f(9) + f(8),f(9) 和 f(8)都需要计算出来,然后再加到备忘录中,如下:

「第二步,」 f(9) = f(8)+ f(7),f(8)= f(7)+ f(6), 因为 f(8) 已经在备忘录中啦,所以可以省掉,f(7),f(6)都需要计算出来,加到备忘录中~

「第三步,」 f(8) = f(7)+ f(6),发现 f(8),f(7),f(6)全部都在备忘录上了,所以都可以剪掉。

所以呢,用了备忘录递归算法,递归树变成光秃秃的树干咯,如下:

带「备忘录」的递归算法,子问题个数=树节点数=n,解决一个子问题还是 O(1),所以「带「备忘录」的递归算法的时间复杂度是 O(n)」。接下来呢,我们用带「备忘录」的递归算法去撸代码,解决这个青蛙跳阶问题的超时问题咯~,代码如下:
public class Solution {
//使用哈希map,充当备忘录的作用
Map<Integer, Integer> tempMap = new HashMap();
public int numWays(int n) {
// n = 0 也算1种
if (n == 0) {
return 1;
}
if (n <= 2) {
return n;
}
//先判断有没计算过,即看看备忘录有没有
if (tempMap.containsKey(n)) {
//备忘录有,即计算过,直接返回
return tempMap.get(n);
} else {
// 备忘录没有,即没有计算过,执行递归计算,并且把结果保存到备忘录map中,对1000000007取余(这个是leetcode题目规定的)
tempMap.put(n, (numWays(n - 1) + numWays(n - 2)) % 1000000007);
return tempMap.get(n);
}
}
}
案例
翻转二叉树
输入:
4
/ \
2 7
/ \ / \
1 3 6 9
输出:
4
/ \
7 2
/ \ / \
9 6 3 1
- 定义函数功能
//翻转一颗二叉树
public TreeNode invertTree(TreeNode root) {
}
/
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
- 寻找递归终止条件
这棵树什么时候不用翻转呢?当然是当前节点为 null 或者当前节点为叶子节点的时候啦。因此,加上终止条件就是:
//翻转一颗二叉树
public TreeNode invertTree(TreeNode root) {
if(root==null || (root.left ==null && root.right ==null)){
return root;
}
}
- 递推函数的等价关系式
原问题之你要翻转一颗树,是不是可以拆分为子问题,分别翻转它的左子树和右子树?子问题之翻转它的左子树,是不是又可以拆分为,翻转它左子树的左子树以及它左子树的右子树?然后一直翻转到叶子节点为止。

首先,你要翻转根节点为 4 的树,就需要「翻转它的左子树(根节点为 2)和右子树(根节点为 7)」。
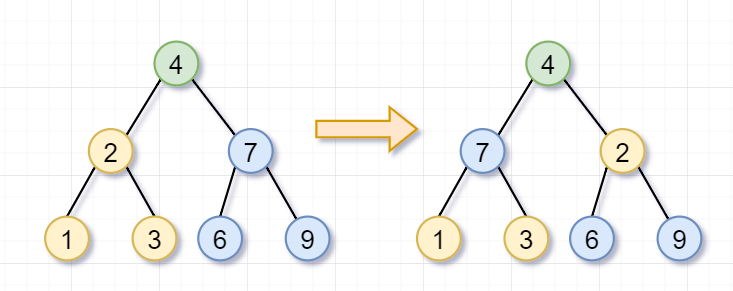
然后呢,根节点为 2 的树,不是叶子节点,你需要继续「翻转它的左子树(根节点为 1)和右子树(根节点为 3)」。因为节点 1 和 3 都是「叶子节点」了,所以就返回啦。

同理,根节点为 7 的树,也不是叶子节点,你需要翻转「它的左子树(根节点为 6)和右子树(根节点为 9)」。因为节点 6 和 9 都是叶子节点了,所以也返回啦。

左子树(根节点为 2)和右子树(根节点为 7)都被翻转完后,这几个步骤就「归来」,即递归的归过程。

显然,「递推关系式」就是:
invertTree(root)= invertTree(root.left) + invertTree(root.right);
于是,很容易可以得出以下代码:
//翻转一颗二叉树
public TreeNode invertTree(TreeNode root) {
if(root==null || (root.left ==null && root.right ==null){
return root;
}
//翻转左子树
TreeNode left = invertTree(root.left);
//翻转右子树
TreeNode right= invertTree(root.right);
}
这里代码有个地方需要注意,翻转完一棵树的左右子树,还要交换它左右子树的引用位置。
root.left = right;
root.right = left;
二叉树路径求和
给一课二叉树,和一个目标值,节点上的值有正有负,返回树中和等于目标值的路径条数,让你编写 pathSum 函数:
/* 来源于 LeetCode PathSum III: https://leetcode.com/problems/path-sum-iii/ */
root = [10,5,-3,3,2,null,11,3,-2,null,1],
sum = 8
10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1
Return 3. The paths that sum to 8 are:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11
递归求解树的问题必然是要遍历整棵树的,所以二叉树的遍历框架(分别对左右孩子递归调用函数本身)必然要出现在主函数 pathSum 中:
- pathSum 函数:给他一个节点和一个目标值,他返回以这个节点为根的树中,和为目标值的路径总数。
- count 函数:给他一个节点和一个目标值,他返回以这个节点为根的树中,能凑出几个以该节点为路径开头,和为目标值的路径总数。
int pathSum(TreeNode root, int sum) {
if (root == null) return 0;
return count(root, sum) +
pathSum(root.left, sum) + pathSum(root.right, sum);
}
int count(TreeNode node, int sum) {
if (node == null) return 0;
return (node.val == sum) +
count(node.left, sum - node.val) + count(node.right, sum - node.val);
}
