微积分基础

1、什么是导数

1.1、导数定义

导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。

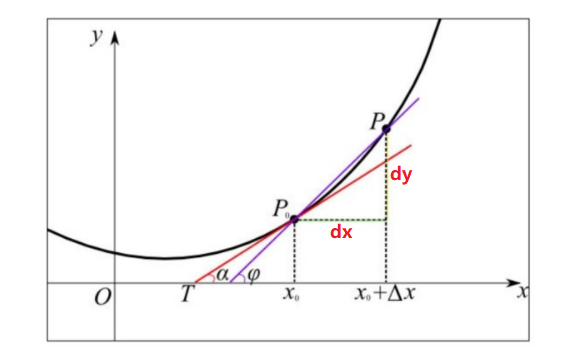
当函数$y = f(x)$的自变量$x$在一点$x_0$上产生一个增量$\Delta x$时，函数输出值的增量$\Delta y$与自变量增量$\Delta x$的比值在$\Delta x$趋于0时的极限limit如果存在，那么，

limit即为函数$f(x_0)$ 在$x_0$ 处的导数，记作$f’(x_0)$ 或$\frac{df(x_0)}{dx}$ 、 $\frac{dy}{dx}$。

$$ f’(x_0) = \lim\limits_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x}=\lim\limits_{\Delta x \rightarrow 0}\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} $$

注意，两者等价：

$$ f’(x_0) =\lim\limits_{\Delta x \rightarrow 0}\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = =\lim\limits_{\Delta x \rightarrow 0}\frac{f(x_0) - f(x_0 - \Delta x)}{\Delta x} $$

推而广之，如果函数全域可导：

$f’(x) =\lim\limits_{\Delta x \rightarrow 0}\frac{f(x + \Delta x) - f(x)}{\Delta x} =\lim\limits_{\Delta x \rightarrow 0}\frac{f(x) - f(x - \Delta x)}{\Delta x}$

高等数学，引入了极限，极限是高等数学的基础，这一点是高等数学与初等数学最大的区别~

1.2、导数作用

求极值，往往设导数为0 ，即可进行求解。

2、左右导数与可导函数

函数趋近于0有两个方向，从左侧趋向于0是左导数，从右侧趋向于0是右导数。

2.1、左导数定义

函数$f(x)$在某点$x_0$的某一左半邻域$(x_0 - \Delta x, x_0)$内有定义，当$\Delta x$从左侧无限趋近于0时，

$\lim\limits_{\Delta x \rightarrow 0}\frac{f(x_0) - f(x_0 - \Delta x)}{\Delta x}$ 的左极限存在，那么就称函数$f(x)$ 在$x_0$ 点有左导数，该极限值就是左导数的值。

2.2、右导数定义

函数$f(x)$在某点$x_0$的某一右半邻域$(x_0,x_0 + \Delta x)$内有定义，当$\Delta x$从右侧无限趋近于0时，

$\lim\limits_{\Delta x \rightarrow 0}\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}$ 的右极限存在，那么就称函数f(x)在$x_0$ 点有右导数，该极限值就是右导数的值。

2.3、左右导数示例

下面的绝对值函数的左导数和右导数不相同，左导数是-1 ，右导数是+1，0位置不可导$f(x) = |x|$ 。

2.4、神经网络激活函数Relu导数

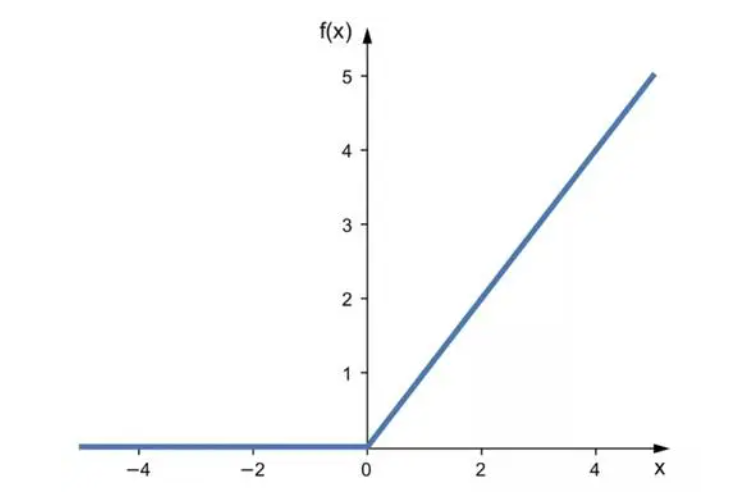
函数如下：

$ f(x) = max(0,x)$

即当$x > 0$时，函数表现为$y = x$；当$x < 0$时，函数表现为$y = 0$ 表现为分段函数的形式：

$f(x) = \left {\begin{aligned} & x \ \ &, x > 0 \ &0\ \ &, x \le 0 \end{aligned}\right.$

则Relu函数的导函数为：

$\frac{d}{dx}f(x) = \left {\begin{aligned} & 1 \ \ &, x > 0 \ &0\ \ &, x \le 0 \end{aligned}\right.$

2.5、可导函数

函数可导的条件如下：

函数在该点的去心邻域内有定义。
函数在该点处的左、右导数都存在。
左导数＝右导数

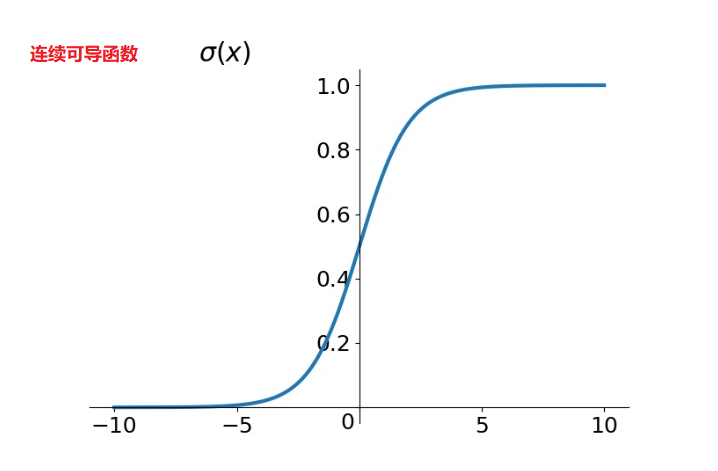
$\sigma(x) = \frac{1}{1 + e^{-x}}$

扩展知识点：

不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。
若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。

可导的函数一定连续；不连续的函数一定不可导。
对于可导的函数$f(x)$， $f’(x)$也是一个函数，称作$f(x)$的导函数（简称导数）。
寻找已知的函数在某点的导数或其导函数的过程称为求导。
求导就是一个求极限的过程，导数的四则运算法则也来源于极限的四则运算法则。
反之，已知导函数也可以倒过来求原来的函数，即不定积分。
微积分基本定理说明了求原函数与积分是等价的。
求导和积分是一对互逆的操作，它们都是微积分学中最为基础的概念。

3、导数的几何与物理含义

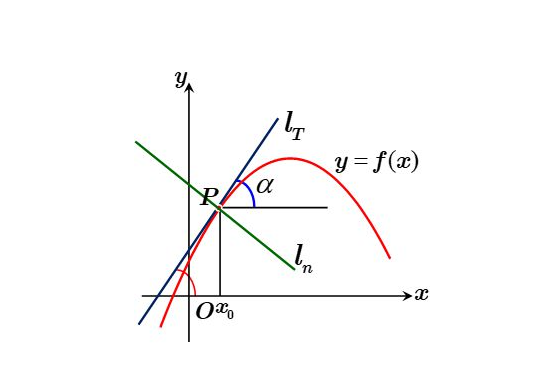
3.1、导数的数学（几何）意义

函数$y = f(x)$在$x_0$点的导数$f’(x_0)$的几何意义：表示函数曲线在点$P(x_0,f(x_0))$ 处的切线的斜率（导数的几

何意义是该函数曲线在这一点上的切线斜率）。

3.2、导数的物理意义

导数可以表示运动物体的瞬时速度和加速度 ，就直线运动而言，位移关于时间的一阶导数是瞬时速度，二阶导数

是加速度。

导数与物理、几何、代数关系密切：在几何中可求切线；在代数中可求瞬时变化率；在物理中可求速度、加速度。

3.3、自由落体示例

自由落体的位移随时间的变化公式如下：

$f(t) = \frac{1}{2}9.8\times t^2$

一阶导数：

v表示速度随时间变化公式

$v = f’(t) = 9.8 \times t$

二阶导数：

$G = f’’(t) = 9.8$

4、函数求导公式

原函数	导函数
$y = C$ ，C是常数	$y’ = 0$
$y = x^n$ ，n是常数且$n \not= 0$	$y’ = nx^{n-1}$
$y = lnx$	$y’ = \frac{1}{x}$
$y = log_ax$ ，$a>0$ 且$a\not=1$	$y’ = \frac{1}{xlna}$
$y = e^x$	$y’ = e^x$
$y = a^x$	$y’ = a^xlna$
$y = \sqrt[n] {x} = x^{\frac{1}{n}}$	$y’ = \frac{1}{n}x^{\frac{1}{n} - 1} = \frac{1}{n}x^{\frac{1-n}{n}}$
$y = \frac{1}{x^n}=x^{-n}$	$y’ = -n\times x^{-n-1} = \frac{-n}{x^{n+1}}$
$y = sin(x)$	$y’ = cos(x)$
……	……

导数的公式都可以根据基本的极限公式进行推导：

$\lim\limits_{n \rightarrow +\infty}(1 +\frac{1}{n})^n = e$

$\lim\limits_{x \rightarrow 0}\frac{sin(x)}{x} = 1$

像这样基本的极限公式还有更多……

三角函数的导数不要管，我们很少会用到它，而且三角函数是周期性函数，而我们的机器学习中很多时候要求是单调的函数，单调增也好，单调减也好，最好不要周期性函数。

5、导数四则运算

导数加减：

$(f(x) \pm g(x))’ = f’(x) \pm g’(x)$

导数乘法：

$(f(x) g(x))’ = f’(x)g(x) + f(x)g’(x)$

导数除法：

$\begin{aligned}(\frac{f(x)}{g(x)})’ &=(f(x)g^{-1}(x))’ \\&=f’(x)g^{-1}(x) + f(x)g^{-1}(x)’\\&=\frac{f’(x)g(x)}{g^2(x)} -f(x)\frac{g’(x)}{g^2(x)}\\&=\frac{f’(x)g(x) - f(x)g’(x)}{g^2(x)}\end{aligned}$

6、复合函数求导法则

一元复合函数$y = f(\psi(x))$ ，$y = f(u)， u = \psi(x)$

其求导有链式法则：

$\frac{dy}{dx} = \frac{dy}{du}\frac{du}{dx}$

画出函数关系图： $y \rightarrow u \rightarrow x$ ，可见从$y$到$x$有一条路径，每一段路径（对应一个导数)乘起来。

这个规则推广到多元复合函数也是适用的。

$(f(g(x)))’ = f’(g)g’(x)$

7、神经网络激活函数求导

7.1、Sigmoid激活函数

$\sigma(x) = \frac{1}{1 + e^{-x}}$

其导函数为：

$\begin{aligned} \sigma’(x) &= \frac{\partial}{\partial x}\frac{1}{1 + e^{-x}} \\&= \frac{e^{-x}}{(1 + e^{-x})^2}\\& = \frac{1}{(1 + e^{-x})^2}\cdot e^{-x}\\&=\frac{1}{1 + e^{-x}} \cdot (1 - \frac{1}{1 + e^{-x}})\\&=\sigma(x)\cdot (1 - \sigma(x))\end{aligned}$

7.2、Tanh激活函数

Tanh函数可以看作是放大并平移的Sigmoid函数，但因为是零中心化的(zero-centered) ，通常收敛速度快于Sigmoid函数，下图是二者的对比：

其函数形式为：

$\begin{aligned}tanh(x) &= \frac{e^x - e^{-x}}{e^x + e^{-x}} \\&= \frac{1 - e^{-2x}}{1 + e^{-2x}} \\&= \frac{2 - (1 + e^{-2x})}{1 + e^{-2x}} \\&= \frac{2}{1 + e^{-2x}} -1 \\&= 2\sigma(2x) - 1\end{aligned}$

其导函数为：

$\begin{aligned}tanh’(x) &= \frac{(e^x + e^{-x})^2 -(e^x - e^{-x})^2}{(e^x + e^{-x})^2} \\&= 1-tanh^2(x)\end{aligned}$

7.3、Softmax激活函数

Softmax函数将多个标量映射为一个概率分布，其形式为：

$y_i = softmax(z_i) = \frac{e^{z_i}}{\sum\limits_{j=1}^{C}e^{z_j}}$

$y_i$ 表示第$i$ 个输出值，即属于类别$i$ 的概率，$\sum\limits_{i = 1}^Cy_i = 1$

$z = W^Tx$ ，表示线性方程，Softmax函数用于多分类，会对应多个方程。

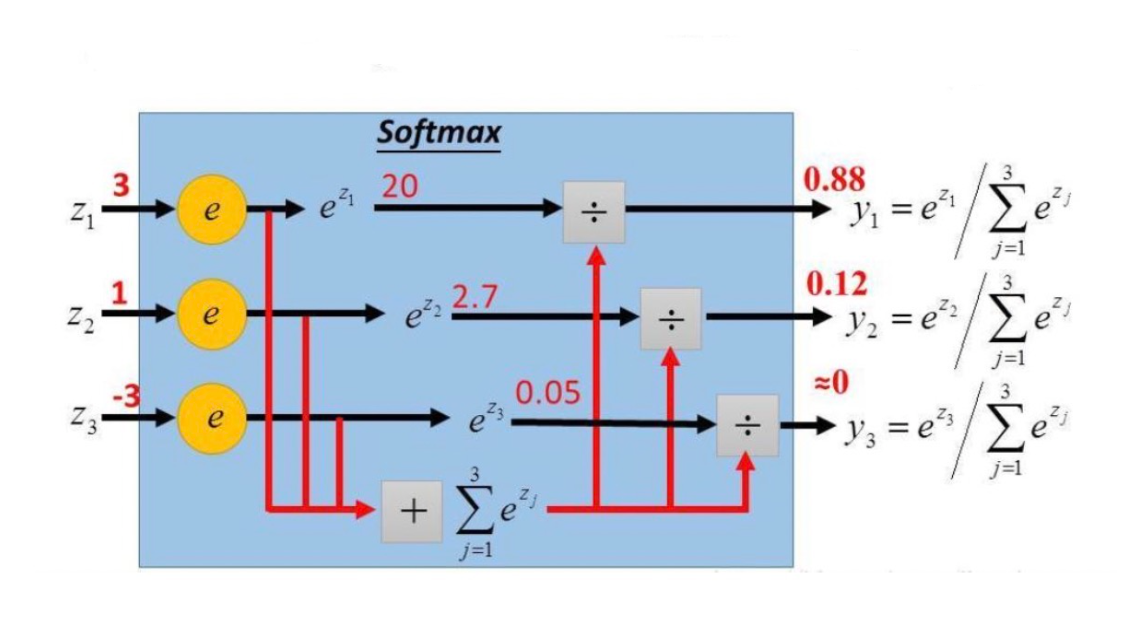
首先求标量形式的导数，即第$i$ 个输出对于第$j$ 个输入的偏导数：

$\frac{\partial y_i}{\partial z_j} = \frac{\partial \frac{e^{z_i}}{\sum\limits_{j=1}^{C}e^{z_j}}}{\partial z_j}$

其中$e^{z_i}$对$z_j$求导要分情况讨论：

$\frac{\partial e^{z_i}}{\partial z_j} = \left {\begin{aligned} & e^{z_i}\ \ , \ \ & if \ \ i = j \ &0\ \ ,\ \ &if \ \ i \not= j \end{aligned}\right.$

那么当$i = j$ 时：

$\begin{aligned}\frac{\partial y_i}{\partial z_j} &= \frac{e^{z_i}\sum\limits_{j=1}^Ce^{z_j} - e^{z_i}e^{z_j}}{(\sum\limits_{j=1}^Ce^{z_j})^2} \\&= \frac{e^{z_i}}{\sum\limits_{j=1}^Ce^{z_j}} - \frac{e^{z_i}}{\sum\limits_{j=1}^Ce^{z_j}}\frac{e^{z_j}}{\sum\limits_{j=1}^Ce^{z_j}} \\&= y_i - y_iy_j\end{aligned}$

当$i \not= j$ 时：

$\frac{\partial y_i}{\partial z_j} = \frac{0 - e^{z_i}e^{z_j}}{(\sum\limits_{j=1}^Ce^{z_j})^2} = -y_iy_j$

两者合并：

$\frac{\partial y_i}{\partial z_j} = \pmb{1}{i=j}y_i - y_iy_j$

其中$\pmb{1}{i=j} = \left{\begin{aligned} & 1, \quad if \ \ i = j \&0,\quad if \ \ i \not= j \end{aligned}\right.$

8、高阶导数

前面学的是一阶导数，对导数再次求导就是高阶导数，二阶和二阶以上的导数统称为高阶导数。

形式如下：

$f’’(x)$

$(f’(x))’$

举个栗子：

$(2x^{10})’ = 20x^9$

$(2x^{10})’’ = (20x^9)’ = 180x^8$

高阶导数形式：

$f^{(n)}(x)$

9、导数与函数单调性

$f’(x) > 0 \quad \uparrow$ $f’(x) < 0 \quad \downarrow$

函数的导数大于0，函数是单调增的。函数的导数小于0，函数是单调减的。

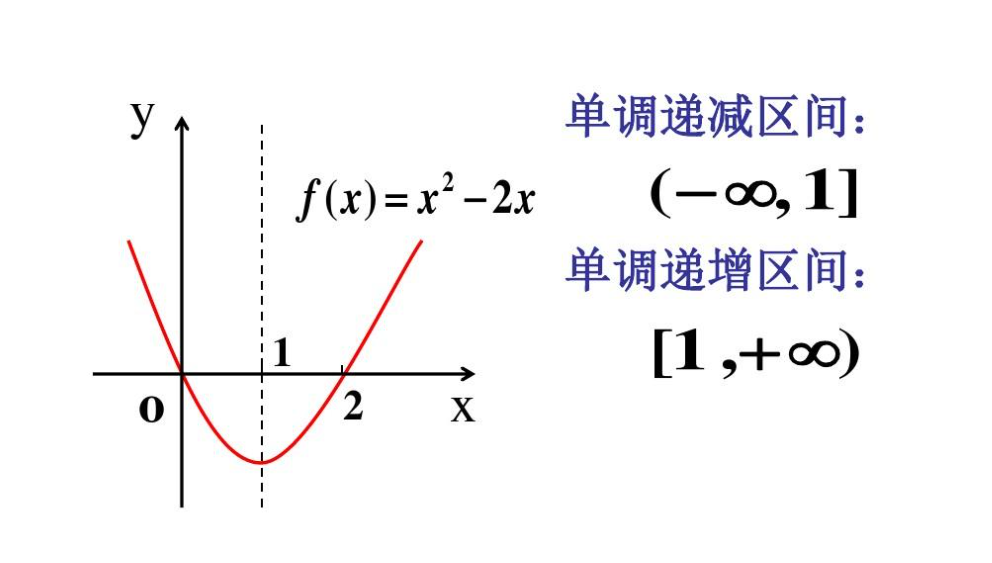
上图函数的导函数如下：

$f’(x) = 2x - 2$

$x < 1$ 时，$f’(x) < 0$ ，函数单调递减
$x > 1$时，$f’(x) > 0$ ，函数单调递增

10、极值定理

导数为我们寻找极值提供依据，对于可导函数而言，因为在极值位置必然有函数的导数等于0。

$f’(x) = 0$

极值处函数的导数等于0，这是必要条件，但不是充分条件，因为极值处的导数必然等于0，但是导数等于0处不代表一定是极值。比如$x$ 的三次方：$f(x) = x^3$

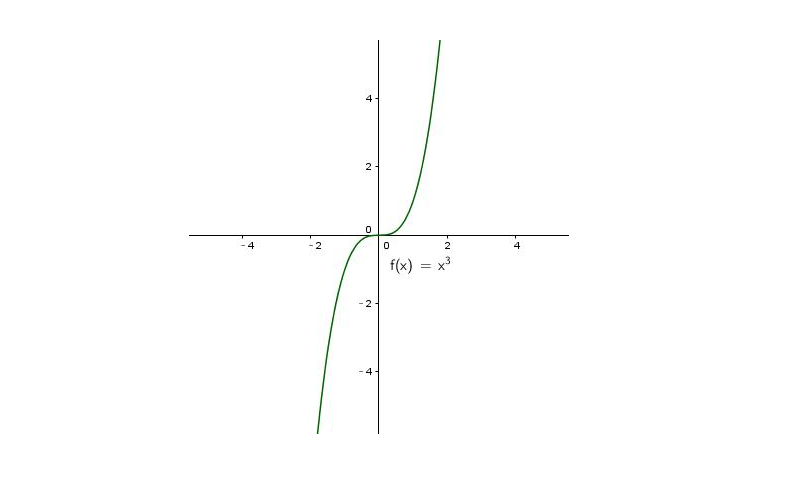
其导数为：

$f’(x)=2x^2$ ，令导数为0，求得x = 0，显然x = 0 ，不是函数的极值！

11、导数与函数凹凸性

11.1、凹凸性概念与判断

函数的二阶导数是和函数的凹凸性是有关系的，凹凸性怎么定义的？

先来做简单的介绍，这里先记住凸函数是向下凸的，反正就是凹的，是否是凸函数可以通过二阶导数，如果二阶

导数是大于0就是凸函数。$f’’(x) > 0 $

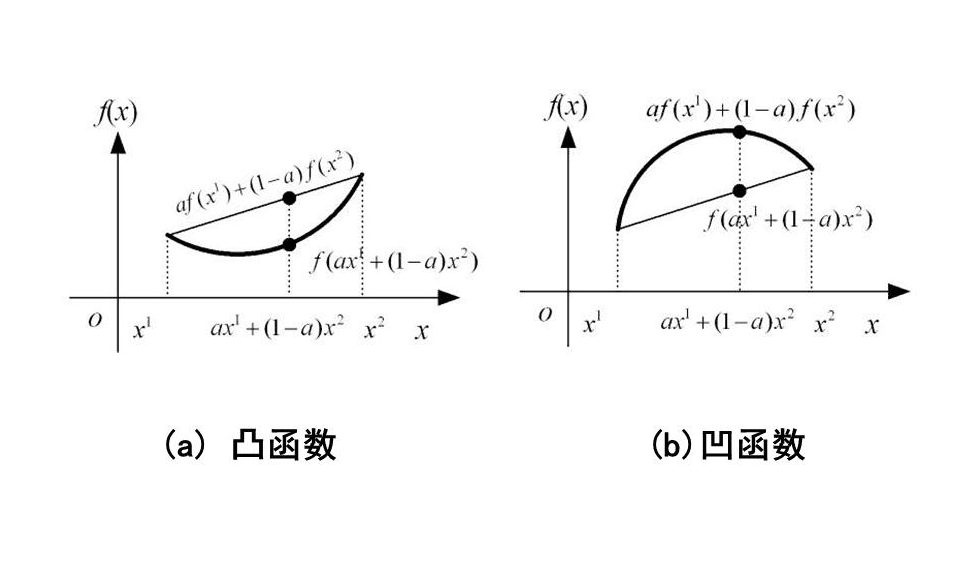
给定函数$f(x) = x^2$ ，其二阶导数是$f’’(x) = 2 > 0 $ ，那么该函数是凸函数。

11.2、知识点拓展

$f’(x) = 0$ ，称之为驻点，驻点是函数增减性的交替点，一侧增一侧减。

$f’’(x) = 0$ ，称之为拐点，拐点是函数凹凸性的交替点，一侧凸一侧凹。

举例说明：

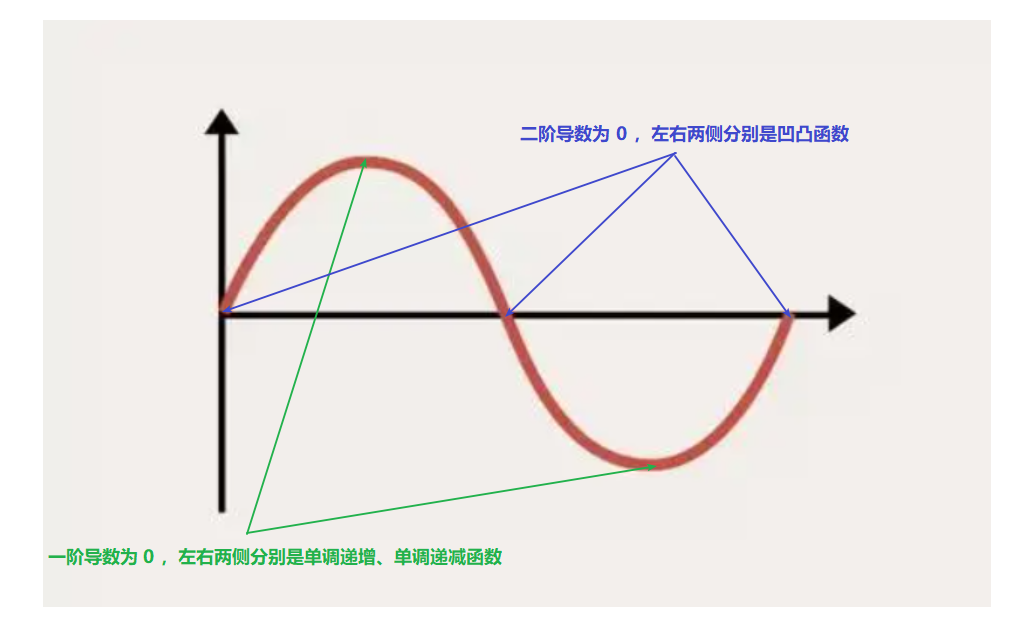
$f(x) = sin(x)$

$f’(x) = cos(x)$，令导数为0 ，左右两侧分别是单调增或单调减。

$f’’(x) = -sin(x)$ ，令导数为0 ，左右两侧分别是凹凸函数。

12、一元函数泰勒展开

若函数$f(x)$在包含$x_0$的某个开区间$(a,b)$上具有$(n +1)$阶导数，那么对于任意$x \in (a,b)$，有：

$f(x) \approx \frac{f(x_0)}{0!} + \frac{f’(x_0)}{1!}(x - x_0) + \frac{f’’(x_0)}{2!}(x-x_0)^2 + \cdot \cdot\cdot + \frac{f^{(n+1)}(x_0)}{(n+1)!}(x-x_0)^{n+1}$

0！= 1可以看做是对于如下规律的完整：

5! = 6!/6
4! = 5!/5

3! = 4!/4
2! = 3!/3

1! = 2!/2

0! = 1!/1 = 1

上述就是泰勒公式，是一个用函数在某点的信息描述其附近取值的公式。如果函数满足一定的条件，泰勒公式可以用函数在某一点的各阶导数值做系数构建一个多项式来近似表达这个函数。

方程变形：

$f(x) = f(x_0 + (x - x_0))$ 其中$(x - x_0)$ 表示一个微小的差值，可以使用$\Delta x$ 表示

$\begin{aligned}f(x_0 + (x - x_0)) &= \frac{f(x_0)}{0!} + \frac{f’(x_0)}{1!}(x - x_0) + \frac{f’’(x_0)}{2!}(x-x_0)^2 + \cdot \cdot\cdot + \frac{f^{(n+1)}(x_0)}{(n+1)!}(x-x_0)^{n+1}\\&=\frac{f(x_0)}{0!} + \frac{f’(x_0)}{1!}\Delta x + \frac{f’’(x_0)}{2!}\Delta x^2 + \cdot \cdot\cdot + \frac{f^{(n+1)}(x_0)}{(n+1)!}\Delta x^{n+1}\end{aligned}$

更加通俗的表示：

$f(x + \Delta x) = \frac{f(x)}{0!} + \frac{f’(x)}{1!}\Delta x + \frac{f’’(x)}{2!}\Delta x^2 + \cdot \cdot\cdot + \frac{f^{(n+1)}(x)}{(n+1)!}\Delta x^{n+1}$

泰勒展开在高等数学里是非常有用的，它可以用来研究函数某些性质完成很多任务。在机器学习里面，它用来求函

数的极值用的，很多时候函数$f(x)$可能会非常复杂，无法直接计算，我们用泰勒展开做一个近似，梯度下降法怎

么做的呢？是做一个近似，保留泰勒展开一阶项。而牛顿法是保留泰勒展开二阶项，忽略二阶以上的项，用泰勒二

阶展开来进行函数$f(x)$近似表达。

一阶泰勒公式：

$f(x + \Delta x) \approx \frac{f(x)}{0!} + \frac{f’(x)}{1!}\Delta x $

二阶泰勒公式：

$f(x + \Delta x) \approx \frac{f(x)}{0!} + \frac{f’(x)}{1!}\Delta x + \frac{f’’(x)}{2!}\Delta x^2$ $$

最近更新于0001-01-01