多元函数微分学
1、多元函数定义
设 D 为一个非空的 n 元有序数组的集合, $f(x)$ 为某一确定的对应规则,也称为函数关系。
$(x_1,x_2,……,x_n) \in D$ 如果对于每一个有序数组,通过对应规则 $f(x)$ 都有唯一确定的实数 $y$ 与之对应,则称对
应规则 $f(x)$ 为定义在 D 上的 n 元函数。记为:
$y = f(x_1,x_2,……,x_n)\ ,\ (x_1,x_2,……,x_n) \in D$ 。变量 $x_1,x_2,……,x_n$ 称为自变量;y 称为因变量。
-
当 n=1 时,为一元函数,记为 $y = f(x)\ ,\ x \in D$ ;
-
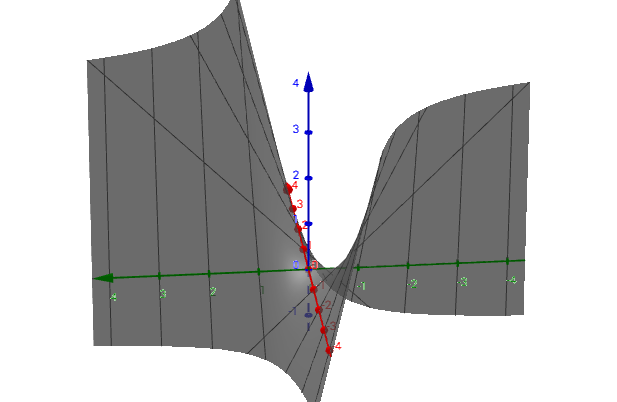
当 n=2 时,为二元函数,记为 $z = f(x,y)\ , \ (x,y) \in D$ ,如图所示:

- 二元及以上的函数统称为多元函数。
2、偏导数
$\frac{\partial f}{\partial x_i} = \lim\limits_{\Delta x_i \rightarrow 0}\frac{f(x_i,…,x_i + \Delta x_i,…,x_n) - f(x_i,…,x_i,…,x_n)}{\Delta x_i}$
偏导数,可以看作是导数的推广,对于多元函数来说,我们把其它的自变量固定不动,看成是常量,我们对其中的某一个变量求导数的话,那就是偏导数了,只对一个变量求导数!
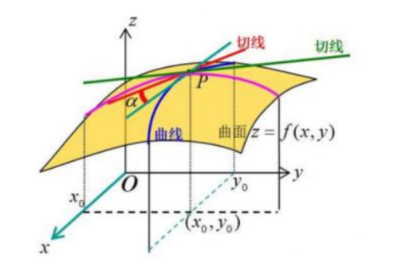
几何意义上面来说就是在某个方向上对原函数来切一下,再去求导,就是偏导数。举例说明:
$f(x,y) = x^2 + 3xy - 2y^2$
对变量 $x$ 求偏导数,其中 $y$ 是常量
$f’x = \frac{\partial f}{\partial x} = 2x + 3y$
对变量 $y$ 求偏导数,则 $x$ 是常量
$f’y = \frac{\partial f}{\partial y} = 3x - 4y$
3、高阶偏导数
有高阶导数,同样也有高阶偏导数,它的情况比高阶导数要复杂一些,因为它的求导变量有多个,比如说:
$\frac{\partial^2f}{\partial x\partial y}$
它对 $x,y$ 求高阶偏导数的话,就是先对 $x$ 求偏导,再对 $y$ 求偏导,其实跟一元函数的高阶导数是一样的,依次对每个变量反复求导即可,我们还是以上面的公式为例:
$f(x,y) = x^2 + 3xy - 2y^2$
二元函数的二阶偏导数有四个:
$\frac{\partial^2 f}{\partial^2 x} = 2$
$\frac{\partial^2 f}{\partial x \partial y} = 3$
$\frac{\partial^2 f}{\partial y \partial x} = 3$
$\frac{\partial^2 f}{\partial^2 y} = -4$
有个重要的结论,就是高阶导数和求导次序无关:
$\frac{\partial^2f}{\partial x\partial y} = \frac{\partial^2f}{\partial y\partial x}$
4、梯度
机器学习中的梯度下降法,和牛顿法很多地方都会用到梯度这个概念。
$\nabla f(x) = \left [ \frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},…,\frac{\partial f}{\partial x_n} \right ]^T $
梯度可以看成一元函数的导数,对于多元函数来说就是偏导数而已。
对于多元函数如果它的自变量有 N 个:$x_1,x_2,……,x_n$ 。它的梯度是个向量,是由对 $x_1,x_2,……,x_n$ 变量
求偏导数构成的这样一个向量,称之为梯度。梯度我们用倒三角这个符号来表示,对 $f(x)$ 求梯度得到上面所示的
向量 $\nabla f(x)$ 。
5、雅可比矩阵
5.1、雅克比矩阵定义
这个可能很多同学学高等数学的时候可能没有学过,但是这个也比较好理解,就是由一阶偏导数构成的矩阵,发明它的目的主要是为了简化求导公式,对多元的复合函数求导,如果我们用雅可比矩阵来计算的话,它会写起来非常简洁,这在我们的人工神经网络反向推导的过程中往往会看到的。
$y = f(x)$ ,其中 $x$ 是 n 维向量表示有 n 个未知数即 n 个自变量,$y$ 是 k 维的向量表示函数对应关系计算返回 k 个因变量。
$y_i = f(x_i)$ ,其中每个 $x_i$ 和每个 $y_i$ 都是相关的,也就是每个 $y_i$ 是单独从 $x_i$ 映射过来的函数。
函数 $f(x)$ 的雅可比矩阵就是每个 $y_i$ 分别对每个 $x_i$ 求偏导,然后构成的矩阵叫做雅可比矩阵:
$\left [\begin{aligned} &\frac{\partial y_1}{\partial x_1},\frac{\partial y_1}{\partial x_2},\cdots,\frac{\partial y_1}{\partial x_n}\&\frac{\partial y_2}{\partial x_1},\frac{\partial y_2}{\partial x_2},\cdots,\frac{\partial y_2}{\partial x_n}\&\ \cdots\ ,\ \cdots\ ,\cdots\ ,\ \cdots\&\frac{\partial y_k}{\partial x_1},\frac{\partial y_k}{\partial x_2},\cdots,\frac{\partial y_k}{\partial x_n}\end{aligned}\right]$
第一行就是 $y_1$ 对 $x_1,x_2,…,x_n$ 求偏导;第二行就是 $y_2$ 对 $x_1,x_2,…,x_n$ 求偏导;第 k 行就是 $y_k$ 对$x_1,x_2,…,x_n$ 求偏导。如果 $x$ 是 n 维向量,$y$ 是 k 个值的因变量,那么雅可比矩阵就是 k*n 的矩阵。
5.2、雅克比矩阵示例
$\left {\begin{aligned}y_1\y_2\end{aligned}\right} \quad\begin{aligned}&y_1 = x_1^2 + 3x_1x_2 + 2x_3\&y_2 = 2x_1 - 2x_1x_2 + x_3^2\end{aligned}\quad \left {\begin{aligned}x_1\x_2\x_3\end{aligned}\right}$
自变量 $x_1,x_2,x_3$ 根据函数 $f(x)$ 映射为因变量 $y_1,y_2$ ,那么 $y_1$ 是 $x_1,x_2,x_3$ 的函数,$y_2$ 也是 $x_1,x_2,x_3$ 的函数,那么函数 $f(x)$ 的雅可比矩阵如下:
$\left[\begin{matrix}&2x_1 + 3x_2,&3x_1,&2 \&2- 2x_2,&-2x_1,&2x_3\end{matrix}\right]$
6、Hessian 矩阵
6.1、Hessian 矩阵定义
Hessian 矩阵是对于一个多元函数来说的,它就相当于一元函数的二阶导数。
有一个关于 $x$ 的 n 元函数 $f(x)$ ,自变量为 $x_1,x_2,…,x_n$ ,那么 Hessian 矩阵为:
$\left [\begin{matrix} &\frac{\partial^2 f}{\partial^2 x_1},&\frac{\partial^2 f}{\partial x_1 \partial x_2},&\cdots,&\frac{\partial^2 f}{\partial x_1 \partial x_n}\&\frac{\partial^2 f}{\partial x_2 \partial x_1},&\frac{\partial^2 f}{\partial^2 x_2},&\cdots,&\frac{\partial^2 f}{\partial x_2 \partial x_n}\&\cdots,&\cdots,&\cdots,&\cdots\&\frac{\partial^2 f}{\partial x_n \partial x_1},&\frac{\partial^2 f}{\partial x_n\partial x_2},&\cdots,&\frac{\partial^2 f}{\partial^2 x_n}\end{matrix}\right]$
Hessian 矩阵是一个 $n*n$ 的矩阵,里面的元素是二阶偏导数构成的。第一个元素是对 $x_1$ 求二阶偏导数,第二个元素是对 $x_1x_2$ 求偏导数,因为咱们前面讲过,多元函数高阶偏导数和顺序无关,所以 Hessian 矩阵是对称矩阵。
6.2、实例演示 Hessian 矩阵
$f(x,y,z) = 3x^2 - 4xy + y^2 - 3z^2$
首先求函数 $f(x,y,z)$ 的一阶偏导数:
- $f’x = 6x -4y$
- $f’y = -4x + 2y$
- $f’z = -6z$
然后求解 Hessian 矩阵:
$\left[\begin{matrix}&6,&-4,&0\&-4,&2,&0\&0,&0,&-6\end{matrix}\right]$
Hessian 矩阵和函数的凹凸性是有密切关系的,如果 Hessian 矩阵正定,可以说函数 $f(x)$ 是凸函数,如果是负定,它就是凹函数 。矩阵正定是如何判定的呢?
7、极值判别法则
7.1、极值判定条件
对于一元函数,我们前面讲过, $f(x)$ 的一阶导数等于 0 处有极值,当 $f(x)$ 的二阶导数大于 0 时是极小值,当 $f(x)$ 的二阶导数小于 0 时是极大值,可以参考 $f(x) = x^2$ 的平方这个函数,其二阶导数是 $f’’(x) = 2 > 0 $ ,那么该函数是凸函数。
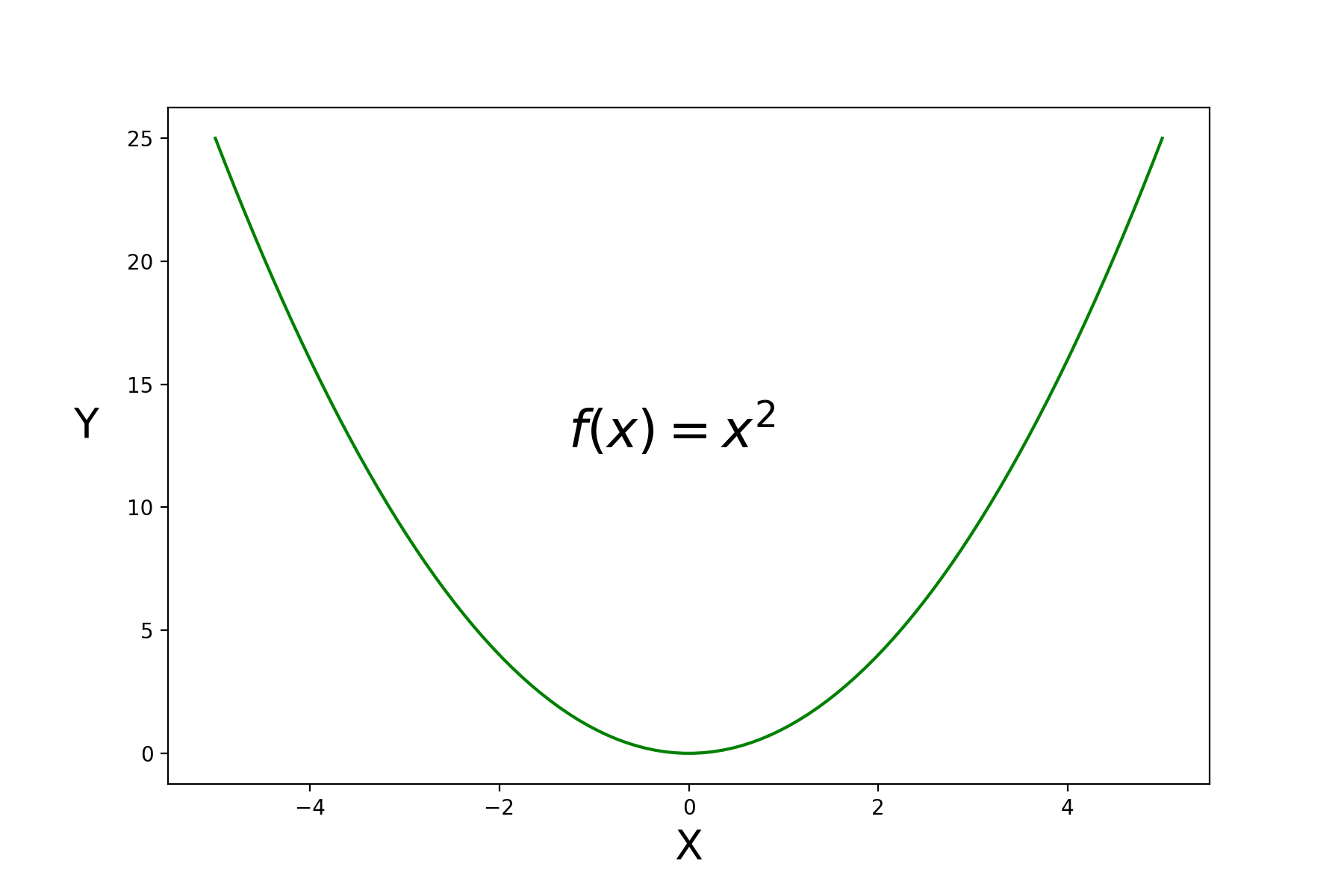
多元函数的极值判别法则,首先 $f(x)$ 的一阶导数等于 0,这点是驻点,那它就可能是极值点,它是极大值还是极小值或者不是极值怎么判定的?
看 Hessian 矩阵,在 $f(x)$ 的一阶导数等于 0 处,就是驻点处。
-
如果 Hessian 矩阵是正定的话,函数在该点有极小值;
-
如果 Hessian 矩阵是负定的话,函数在该点有极大值;
-
如果 Hessian 矩阵不定,函数在该点不是极值;
7.2、实对称矩阵正定负定判定
实对称矩阵 A 正定负定判定条件:
- 对于任意向量 $\vec{v} \not= 0$,都有 $\vec{v}^TA\vec{v} > 0$ ,那么 A 就是正定矩阵;
- 对于任意向量 $\vec{v} \not= 0$,都有 $\vec{v}^TA\vec{v} < 0$ ,那么 A 就是负定矩阵;
实对称矩阵 A 负定,代码演示:
import numpy as np
A = np.array([[-2,-3,-1],
[-3,-6,-4],
[-1,-4,-5]])
v = np.array([3,5,6])
print('给定向量任意向量v:',v)
print('求解矩阵A正定判定条件结果是:',v.dot(A).dot(v))
'''
给定向量任意向量v: [3 5 6]
求解矩阵A正定判定条件结果是: -714
'''
实对称矩阵 A 正定,代码演示:
import numpy as np
A = np.array([[5,1,-4],
[1,3,-2],
[-4,-2,7]])
v = np.array([-5,2,-3])
print('给定向量任意向量v:',v)
print('求解矩阵A正定判定条件结果是:',v.dot(A).dot(v))
'''
给定向量任意向量v: [ 2 -3 -5]
求解矩阵A正定判定条件结果是: 128
'''
但是这样不太容易判断,我们还可以根据特征值正负去判断矩阵正定与否:
- 矩阵 A 的特征值全部大于 0,那么矩阵 A 为正定矩阵;
- 矩阵 A 的特征值全部小于 0,那么矩阵 A 为负定矩阵;
实对称矩阵 A 负定,特征值代码演示:
import numpy as np
A = np.array([[-2,-3,-1],
[-3,-6,-4],
[-1,-4,-5]])
w,v = np.linalg.eig(A)
print('矩阵A的特征值特征向量是:')
display(w,v)
'''
矩阵A的特征值特征向量是:
array([-10.54287655, -0.03922866, -2.41789479])
array([[ 0.32798528, 0.73697623, -0.59100905],
[ 0.73697623, -0.59100905, -0.32798528],
[ 0.59100905, 0.32798528, 0.73697623]])
'''
实对称矩阵 A 正定,特征值代码演示:
import numpy as np
A = np.array([[5,1,-4],
[1,3,-2],
[-4,-2,7]])
w,v = np.linalg.eig(A)
print('矩阵A的特征值特征向量是:')
display(w,v)
'''
矩阵A的特征值特征向量是:
array([10.74515039, 1.63251546, 2.62233415])
array([[-0.58123713, -0.60851363, -0.54025416],
[-0.27299496, -0.4796241 , 0.83392714],
[ 0.76657495, -0.63219608, -0.11265418]])
'''
8、二次型
8.1、二次型定义
二次型就是纯二次项构成的一个函数 。
因为二次函数(方程)的二次部分最重要,为了方便研究,我们把含有 n 个变量的二次齐次函数:
$f(x_1,x_2,\cdots,x_n) = a_{11}x_1^2 + a_{22}x_2^2 + \cdots + a_{nn}x_n^2 + 2a_{12}x_1x_2 + 2a_{13}x_1x_3+\cdots + 2a_{n-1,n}x_{n-1}x_n$
称为二次型。
8.2、二次型表示
我们可以通过矩阵来进行表示

二次型通俗表现形式:
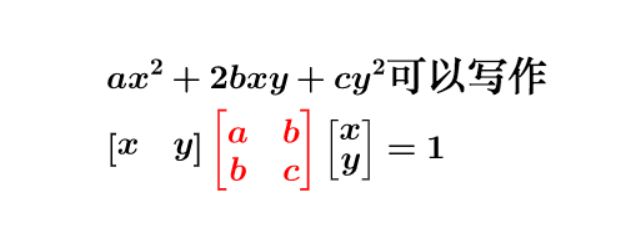
二次型矩阵表示:
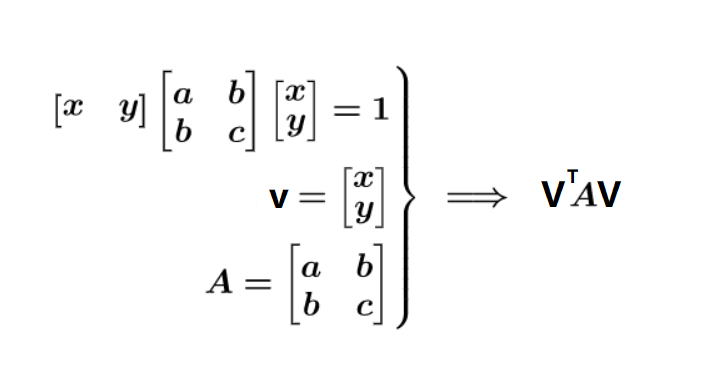
n 个变量的二次齐次函数矩阵表示:
$f(x_1,x_2,\cdots,x_n) = a_{11}x_1^2 + a_{22}x_2^2 + \cdots + a_{nn}x_n^2 + 2a_{12}x_1x_2 + 2a_{13}x_1x_3+\cdots + 2a_{n-1,n}x_{n-1}x_n$
$x^TAx$
$[x_1,x_2,\cdots,x_n]\left[\begin{matrix}&a_{11}\quad a_{12}\quad \cdots \quad a_{1n}\&a_{21}\quad a_{22}\quad\cdots\quad a_{2n}\&\cdots\quad\cdots\quad\cdots\quad\cdots\&a_{n1}\quad a_{n2}\cdots\quad a_{nn}\end{matrix}\right]\left[\begin{matrix}x_1\x_2\\cdots\x_n\end{matrix}\right]$
8.3、二次型应用
在机器学习中,我们可以根据数据分布进行模型选择:
- 如果数据分布是一次型的,那我们就可以选择 Logistic Regression、SVM 等分界面为一次型的模型;
- 如果数据分布是二次型的,我们可以选择 naive bayes;
- 如果数据分布既不是一次型也不是二次型,那我们可以选择基于决策树的模型,例如 GBDT、随机森林等,或者 DNN(深度神经网络),这些模型都高度非线性,表达能力极强理论上可以拟合任意曲线。
8.4、Hessian 矩阵与二次型
$A = \left [\begin{matrix} &\frac{\partial^2 f}{\partial^2 x_1},&\frac{\partial^2 f}{\partial x_1 \partial x_2},&\cdots,&\frac{\partial^2 f}{\partial x_1 \partial x_n}\&\frac{\partial^2 f}{\partial x_2 \partial x_1},&\frac{\partial^2 f}{\partial^2 x_2},&\cdots,&\frac{\partial^2 f}{\partial x_2 \partial x_n}\&\cdots,&\cdots,&\cdots,&\cdots\&\frac{\partial^2 f}{\partial x_n \partial x_1},&\frac{\partial^2 f}{\partial x_n\partial x_2},&\cdots,&\frac{\partial^2 f}{\partial^2 x_n}\end{matrix}\right]$
将 Hessian 矩阵 A 转换为二次型:
$f(x) = \vec{x}^TA\vec{x}$ ,其中 $\vec{x}$ 表示非零任意向量
- $f(x) > 0,\quad \vec{x} \not=0,\quad x \in R$ ,则 $f(x)$ 为正定二次型,A 为正定矩阵
- $f(x) \ge 0,\quad \vec{x} \not=0,\quad x \in R$ ,则 $f(x)$ 为半正定二次型,A 为半正定矩阵
- $f(x) < 0,\quad \vec{x} \not=0,\quad x \in R$ ,则 $f(x)$ 为负定二次型,A 为负定矩阵
- $f(x) \le 0,\quad \vec{x} \not=0,\quad x \in R$ ,则 $f(x)$ 为半负定二次型,A 为半负定矩阵
- 以上皆不是,就叫做不定
正定效果图,如下所示:

半正定效果图,如下:

不定效果图,如下: