贝叶斯理论
贝叶斯理论
贝叶斯定理缘起于托马斯.贝叶斯(1702-1761),一位英国长老会牧师和业余数学家。在他去世后发表的论文论有关机遇问题的求解中,贝叶斯定理的现代形式实际上归因于拉普拉斯(1812)。拉普拉斯重新发现了贝叶斯定理,并把它用来解决天体力学、医学甚至法学的问题。但自 19 世纪中叶起,随着频率学派的兴起,概率的贝叶斯解释逐渐被统计学主流所拒绝。
现代贝叶斯统计学的复兴肇始于 Jeffreys(1939), 在 1950 年代,经过 Wald(1950), Savage(1954), Raiffic&Schlaifer(1961), Lindley(1972), De Finetti(1974) 等人的努力,贝叶斯统计学逐渐发展壮大,并发展出了贝叶斯统计决策理论这个新分支。特别是到 1990 年代以后,随着计算方法 MCMC 在贝叶斯统计领域的广泛应用,解决了贝叶斯统计学长期存在的计算困难的问题,从而推动了贝叶斯统计在理论和应用领域的长足发展。贝叶斯统计学广泛应用于各个学科。就本书的主题而言,从认知学科、政治学到从自然语言处理和社会网络分析,贝叶斯方法都起到了举足轻重的作用。
贝叶斯思维模式
在我们孩提时代,爸妈希望教会我们某个词汇的含义时,他们首先会给我们展示很多的正例。譬如对于狗这个单词,爸妈可能会说:看那条狗狗好可爱,或者,小心狗狗。不过爸妈不会像机器一样给我们展示所谓的负例,他们不会指着一只猫说:这货不是狗,最多就是当孩子们认错的时候,父母会予以纠正。心理学家研究表明,人们可以单纯地从正例中学习概念,而不一定需要负例的介入。而这种认知单词的学习过程可以抽象概括为所谓的概念学习(Concept Learning ),在某些意义上很类似于二元分类。譬如我们可以定义当 $x$ 为某个概念 C 的实例时 $f(x) = 1$,否则 $f(x) = 0$。而学习的过程即是构建这个指示函数 $f$,该函数定义了哪些元素属于概念 C。当我们允许这个函数具有一定的不确定性时,我们就可以通过概率计算得出所谓的模糊集(Fuzzy Set )。还需要提到的是,标准的二维分类是同时需要正负例存在的,不过我们也可以单纯地从正例中学习。阐述完了基本的概念,接下来我们会以一个简单的数字游戏来进行形象化的说明,这里我们随便选定几个数学上的概念作为学习目标。譬如我们可以将概念 C 定义为所有的素数,或者介于 1~10 之间的数字。然后给你多组随机从 C 中抽样出的正数序列:$D = {x_1,…,x_N}$,然后给你一个新的测试序列 $ \widetilde{x} $ 让你判断其应该归属于哪个概念。
上图四组对比数据分别显示了给不同的组选定不同的观测集合时他们推导出的概念 C 的数字分布。前两行是分别展示了 $D = {16}$ 与 $D = {60}$,会发现得出的结果非常分散(这里选定的数字范围为 1~100)。而第三行中观测数据为 $D = {16,8,2,64}$,人们得出了一定的规律,即选定了 2 的方幂值。而最后一行中给出的观测数据是 $D = {16,23,19,20}$,人们得出的规律是选定靠近 20 的数字。我们来复盘每个组的思考过程,譬如当首先给出 $16$ 作为观测数据时,人们可能会选择 17?因为 17 离 16 最近,也有可能会选择 6,因为它们的个位数都是 6. 当然也有可能是 32,因为它们都是 2 的方幂值,不过估计是没啥人会选择 99 的。从这样简单地思考过程我们可以得出一个结论,显而易见的部分数字被选中的概率是大于其他数字的,这种概率就可以表示为某个概率分布:$p(\widetilde{x} | D)$。这个概率就是所谓的后验概率,表示了在给定观测值 $D$ 的情况下每个数字属于 D 的概念集 $\widetilde{x} ~ C$ 的概率。接下来如果继续给出 $8,2,64$ 作为正例,那么我们会猜测隐藏的概念为 2 的方幂值,这种思考过程就是典型的归纳(Induction )。而如果继续给出 $23,19,20$ 作为正例,那么我们会得出另一个完全不同的泛化梯度(Generalization Gradient )的结果。机器学习的任务就是将上述思考的过程转化为机器计算,经典的在让机器进行数学归纳的方法就是我们先预置很多概念的假设空间 $H$(Hypothesis Space ),譬如:奇数、偶数、1~100 之间的数字、2 的方幂、所有以 6 结尾的数字等等。而与观测值 $D$ 相符的 $H$ 的子集称为样本空间(Version Space )。譬如在上面的思考过程中,随着样本空间的增长我们越发坚定了对于某个概念的信心。不过样本空间往往会很多且重复,譬如上文中如果 $D={16}$,其与很多假设空间都存在一致的样本空间,又该如何抉择呢?
贝叶斯定理
贝叶斯定理,也称为贝叶斯法则现在是概率论教科书的重要内容。一般我们习惯于它的离散(事件)形式:
$$ P(A_i|B) = \frac{P(B|A_i)P(A_i)}{ \sum{P(B|A_j)P(A_j)}} $$
其中
- $B$ 称为观测变量
- $A_i$ 称为参数 / 隐变量
- $P(A_i)$ 称为先验概率,表示在对样本观测前我们关于这个问题已经具有的知识
- $P(A_i|B)$ 称为后验概率,是在进行了新观测之后对原有知识的更新
- $P(B|A_i)$ 称为似然。
- $P(B) = \sum{P(B|A_j)P(A_j)}$ 称为 Evidence,即数据是由该模型得出的证据

贝叶斯理论应用
贝叶斯定理作为一种概率计算可用于多个领域内进行概率推理。今天,我们用贝叶斯法则过滤垃圾邮件,为网站用户推荐唱片、电影和书籍。它渗透到了互联网、语言和语言处理、人工智能、机器学习、金融、天文学和物理学乃至国家安全等各个领域。
在真实的机器学习任务中,我们往往是需要在训练集上得出似然函数值。譬如对上述盒子与球模型中,我们将问题重新叙述为:我们的训练集中有多个方形与圆形的盒子,每个盒子中含有不定数量的红黄白三种颜色的小球。那么此时问题就抽象为了 : 当你观察一个事件 $X$,你预估计并给出其内部参数 $\theta$,表示你对于事件 $X$ 发生的置信程度。
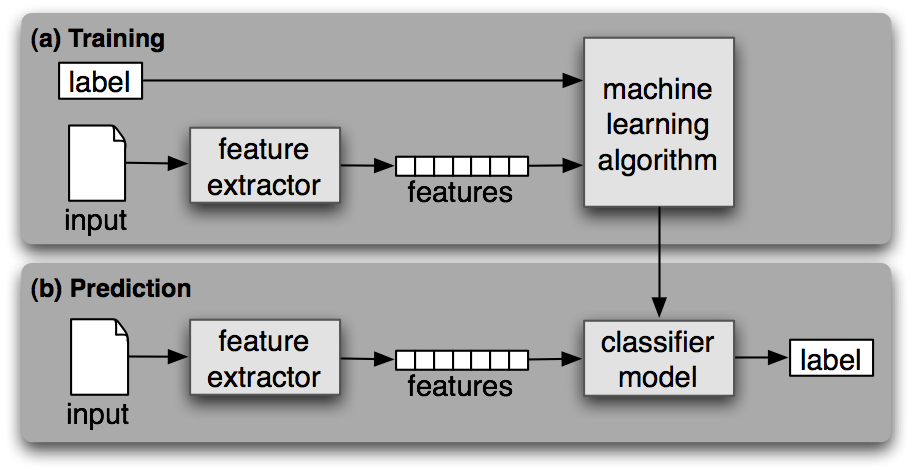
贝叶斯理论最基础的使用就是在分类问题中,也就是所谓的生成式分类器(Generative Classifier),其基本形式如下所示:
$$ p(y = c | \vec{x},\vec{\theta}) \propto p(\vec{x} | y = c, \vec{\theta}) p(y = c | \vec{\theta}) $$
在训练阶段,我们基于带有标签的训练集的辅助来寻找合适的类条件概率/似然概率:
$$ p(\vec{x} | y = c, \vec{\theta}) $$
并且推导出模型参数 $\vec{\theta}$,其定义了我们期望在某类中出现某类型数据的概率。最后在预测阶段,我们基于类条件概率/似然概率来计算数据 $\vec{x}$ 从属于各个类的后验概率,并且选择概率最大的为其预测值。
