最小二乘法

最小平方法是十九世纪统计学的主题曲。从许多方面来看,它之于统计学就相当于十八世纪的微积分之于数学。

案例：尺子估算

来看一个生活中的例子。比如说，有五把尺子：

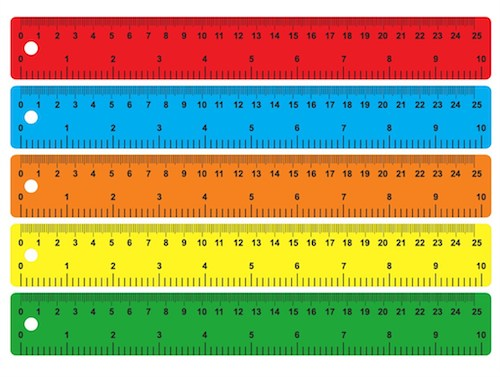
用它们来分别测量一线段的长度，得到的数值分别为（颜色指不同的尺子）：

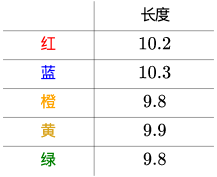
总之就是有误差，这种情况下，一般取平均值来作为线段的长度：

$$ \bar{x}=\frac{10.2+10.3+9.8+9.9+9.8}{5}=10 $$

换一种思路来思考刚才的问题，首先，把测试得到的值画在笛卡尔坐标系中，分别记作$y_i$：

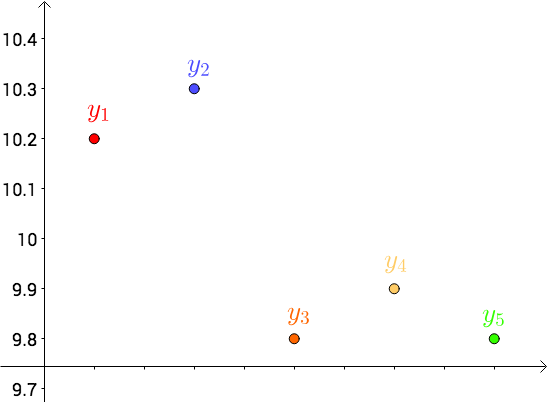
其次，把要猜测的线段长度的真实值用平行于横轴的直线来表示（因为是猜测的，所以用虚线来画），记作$y$：

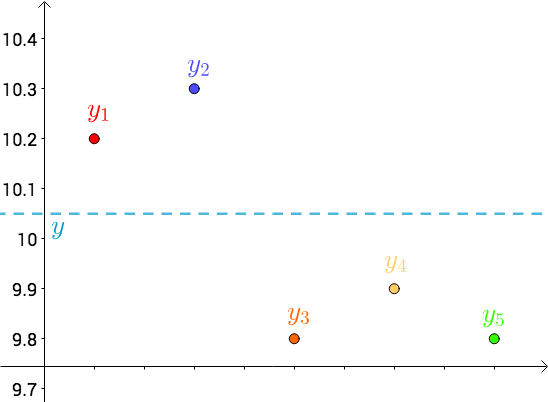
每个点都向$y$做垂线，垂线的长度就是$|y-y_i|$，也可以理解为测量值和真实值之间的误差：

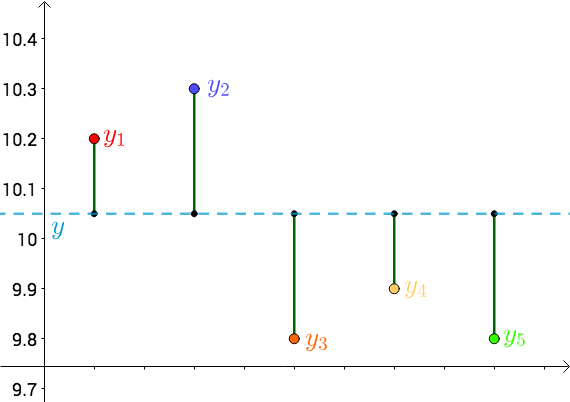
因为误差是长度，还要取绝对值，计算起来麻烦，就干脆用平方来代表误差：

$$ \left|y-y_{i}\right| \rightarrow\left(y-y_{i}\right)^{2} $$

总的误差的平方就是：

$$ \epsilon=\sum\left(y-y_{i}\right)^{2} $$

因为$y$是猜测的，所以可以不断变换，自然，总的误差\epsilon也是在不断变化的。法国数学家，阿德里安-馬里·勒讓德（1752－1833，这个头像有点抽象）提出让总的误差的平方最小的y就是真值，这是基于，如果误差是随机的，应该围绕真值上下波动：

$$ \epsilon=\sum\left(y-y_{i}\right)^{2} \text {最小} \Longrightarrow \text {真值} y $$

这是一个二次函数，对其求导，导数为0的时候取得最小值：

$$ \begin{aligned} \frac{d}{d y} \epsilon &=\frac{d}{d y} \sum\left(y-y_{i}\right)^{2}=2 \sum\left(y-y_{i}\right) \ &=2\left(\left(y-y_{1}\right)+\left(y-y_{2}\right)+\left(y-y_{3}\right)+\left(y-y_{4}\right)+\left(y-y_{5}\right)\right)=0 \end{aligned} $$

进而：

$$ 5 y=y_{1}+y_{2}+y_{3}+y_{4}+y_{5} \Longrightarrow y=\frac{y_{1}+y_{2}+y_{3}+y_{4}+y_{5}}{5} $$

以下这种方法：

$$ \epsilon=\sum\left(y-y_{i}\right)^{2} \text {最小} \Longrightarrow \text {真值} y $$

就是最小二乘法，所谓“二乘”就是平方的意思，台湾直接翻译为最小平方法。

最小二乘法

最小二乘法

案例：尺子估算

Links