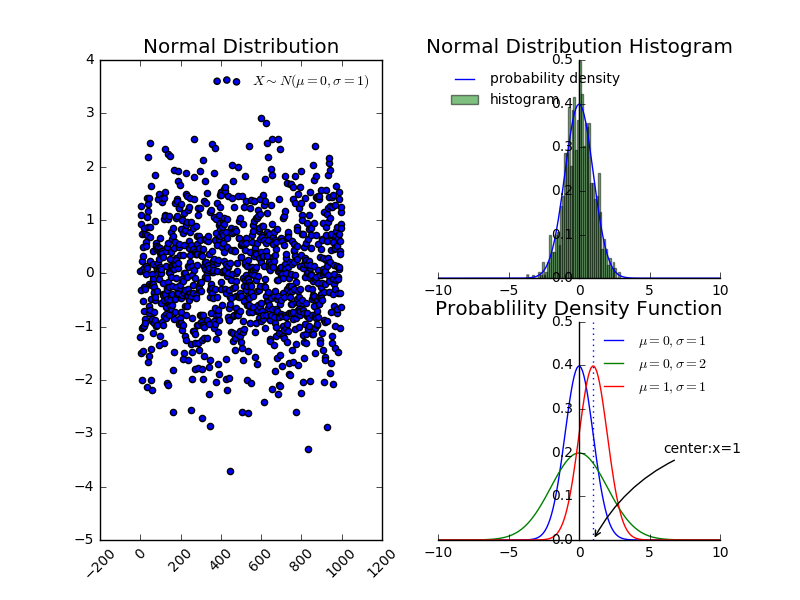
正态分布/高斯分布

正态分布只依赖于数据集的两个特征：样本的均值和方差。正态分布的这种统计特性使得问题变得异常简单，任何具有正态分布的变量，都可以进行高精度分预测。值得注意的是，大自然中发现的变量，大多近似服从正态分布。即如果某个随机变量取值范围是实数，且对它的概率分布一无所知，通常会假设它服从正态分布，其考量的原因包括：

• 中心极限定理表明，多个独立随机变量的和近似正态分布，则建模的任务的真实分布通常都确实接近正态分布。

• 在具有相同方差的所有可能的概率分布中，正态分布的熵最大（即不确定性最大）。

一维正态分布

设$X \sim N(\mu,\sigma^2)$，则其概率密度为：

$$ f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}, -\infty<x<\infty $$

其中$\mu, \sigma(\sigma>0)$为常数，若随机变量$X$的概率密度函数如上所述，则称$X$服从参数为$\mu, \sigma$的正态分布或者高斯分布，记作$X \sim N\left(\mu, \sigma^{2}\right)$。

当$\mu=0, \sigma=1$时，称为标准正态分布，其概率密度函数记作$\varphi(x)$，分布函数记作$\Phi(x)$。为了方便计算，有时记作$\mathcal{N}\left(x ; \mu, \beta^{-1}\right)=\sqrt{\frac{\beta}{2 \pi}} \exp \left(-\frac{1}{2} \beta(x-\mu)^{2}\right)$，其中$\beta \in(0, \infty)$。

正态分布的概率密度函数性质如下：

• 曲线关于$x = \mu$处对称，并且在该处取到最大值。
• 曲线在$x=\mu \pm \sigma$处有拐点，参数$\mu$决定曲线的位置，$\sigma$决定图形的胖瘦。

若$X \sim N\left(\mu, \sigma^{2}\right)$则称$\frac{X-\mu}{\sigma} \sim N(0,1)$，其期望$\mathbb{E}[X]=\mu$，方差$\operatorname{Var}[X]=\sigma^{2}$。

有限个相互独立的正态随机变量的线性组合仍然服从正态分布：若随机变量$X_{i} \sim N\left(\mu_{i}, \sigma_{i}^{2}\right), i=1,2, \cdots, n$，且它们相互独立，则它们的线性组合：$C_{1} X_{1}+C_{2} X_{2}+\cdots+C_{n} X_{n}$仍然服从正态分布（其中$C_{1}, C_{2}, \cdots, C_{n}$不全是为0的常数），且$C_{1} X_{1}+C_{2} X_{2}+\cdots+C_{n} X_{n} \sim N\left(\sum_{i=1}^{n} C_{i} \mu_{i}, \sum_{i=1}^{n} C_{i}^{2} \sigma_{i}^{2}\right)$。

多维正态分布

https://parg.co/NOA 5.4节

二维正态随机变量$(X,Y)$的概率密度为：

$$ \begin{aligned} p(x, y) &=\frac{1}{2 \pi \sigma_{1} \sigma_{2} \sqrt{1-\rho^{2}}} \exp \left{\frac{-1}{2\left(1-\rho^{2}\right)}\left[\frac{\left(x-\mu_{1}\right)^{2}}{\sigma_{1}^{2}}\right.\right.\ &-2 \rho \frac{\left(x-\mu_{1}\right)\left(y-\mu_{2}\right)}{\sigma_{1} \sigma_{2}}+\frac{\left(y-\mu_{2}\right)^{2}}{\sigma_{2}^{2}} ] } \end{aligned} $$

根据定义，可以计算出:

$$ p_{X}(x)=\frac{1}{\sqrt{2 \pi} \sigma_{1}} e^{-\left(x-\mu_{1}\right)^{2} /\left(2 \sigma_{1}^{2}\right)},-\infty<x<\infty \ p_{Y}(y)=\frac{1}{\sqrt{2 \pi} \sigma_{2}} e^{-\left(y-\mu_{2}\right)^{2} /\left(2 \sigma_{2}^{2}\right)},-\infty<y<\infty \ $$

$$ \begin{array}{c}{\mathbb{E}[X]=\mu_{1}} \ {\mathbb{E}[Y]=\mu_{2}} \ {\operatorname{Var}[X]=\sigma_{1}^{2}} \ {\operatorname{Var}[Y]=\sigma_{2}^{2}} \ {\operatorname{Cov}[X, Y]=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}\left(x-\mu_{1}\right)\left(y-\mu_{2}\right) p(x, y) d x d y=\rho \sigma_{1} \sigma_{2}} \ {\rho_{X Y}=\rho}\end{array} $$

多维正态随机变量

拉普拉斯分布

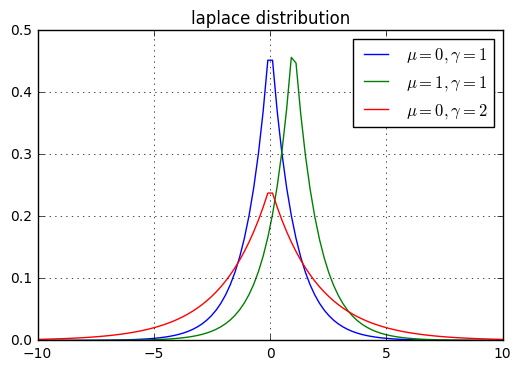
拉普拉斯分布的概率密度函数为：

$$ p(x ; \mu, \gamma)=\frac{1}{2 \gamma} \exp \left(-\frac{|x-\mu|}{\gamma}\right) $$

其期望为$\mathbb{E}[X]=\mu$，方差为$\operatorname{Var}[X]=2 \gamma^{2}$。