56-GRU

56-门控循环单元(GRU)

1. 动机：如何关注一个序列

• 不是每个观察值都是同等重要

比如上图中的序列，若干个猫中出现了一个鼠，那么我们应该重点关注这个鼠，而中间重复出现的猫则减少关注。文本序列同理，通常长文本我们需要关注的是几个关键词，关键句。

• 想只记住相关的观察需要：
  • 能关注的机制（更新门）：顾名思义，是否需要根据我的输入，更新隐藏状态
  • 能遗忘的机制（重置门）：更新候选项时，是否要考虑前一隐藏状态。

2. 门的概念

• 更新门 Zt，重置门 Rt 的公式大体相同，唯一不同的是学习到的参数。

• 需要注意的是，计算门的方式和原来 RNN 的实现中计算新的隐状态相似，只是激活函数改成了 sigmoid。

• 门本来是电路中的一个概念，0,1 代表不同的电平，可以用于控制电路的通断。此处 sigmoid 将门的数值归一化到 0 到 1 之间，是一种"软更新"方式。而从后面的公式上可以看出，本讲课程采用的是低电平有效（越靠近 0，门的作用越明显）的方式控制。

3. 候选隐状态

• 候选隐状态，如果抛开公式中的$R_{t}$遗忘门来说，这个和之前 RNN 中计算当前步的隐状态没有差别。

• 但是这里引入了遗忘门，如果$R_{t}$无限接近于 0，那么此时候选隐状态将不再考虑前一隐状态的影响，也就是和 MLP 没有区别，起到“遗忘”的作用；

• 反之，如果$R_{t}$无限接近于 1，那么与 RNN 计算隐状态的过程没有差别，不进行遗忘。

• 公式中的 ⊙ 表示逐元素乘积。

为什么叫候选隐状态？

在 RNN 中，这个所谓的候选隐状态就是当前步的隐状态（$R_{t}$无限接近 1 时）。但是由于引入了更新门，我们需要考虑是直接沿用上一步的隐藏状态，还是像 RNN 一样使用当前步计算的隐状态。所以这个结合了当前输入计算的隐状态，不能立马变成当前的$H_{t}$，而是需要用更新门和前一隐状态$H_{t-1}$做一个加权，所以它是一个候选项。

4. 隐状态

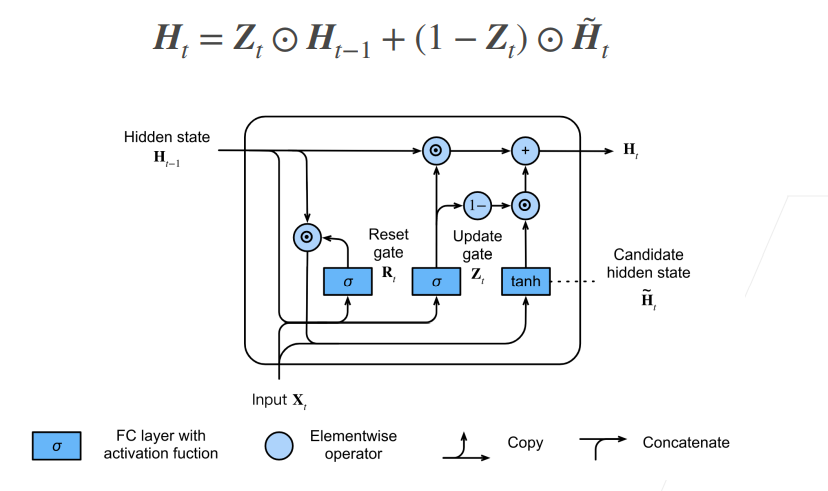
用更新门对候选隐状态和前一隐状态做加权，得到当前步隐状态的值。

如果$Z_{t}$无限接近于 0，更新起作用，候选隐状态“转正”，变为当前隐状态。

如果$Z_{t}$无限接近于 1，更新不起作用，当前隐状态还是沿用前一隐状态。

5. 总结

上图四行公式概括了 GRU 模型。在 RNN 的基础上，最重要的是引入了更新门和重置门，来决定前一隐状态对当前隐状态的影响。以最开始的猫鼠序列的例子来说，如果我的模型一直看到猫，模型可以学习到隐状态不怎么去更新，于是隐状态一直保留了猫的信息，而看到老鼠，隐状态才进行更新。

• 对于一个更具体的例子而言(语言模型)：

“The cat, which already ate ……, __(is/ was) full.”，假设我的句子很长，预测完前面的词后需要预测下一个词 is 还是 was，如果引入这种更新/重置的机制，那我们的模型可以在 was 这个词之前尽可能去保持隐状态的信息，从而即使阅读了一个很长的定语从句，但我们还是保留了 cat 这个词的单数信息，从而模型预测下一个词为’was’。

• 一个与 RNN 的联动在于：

如果更新门完全发挥作用（无限接近于 0），重置门不起作用（无限接近于 1），此时 GRU 模型退化为 RNN 模型。

6. QA

问题：GRU 为什么需要两个门？

重置门和更新门各司其职。重置门单方面控制自某个节点开始，之前的记忆（隐状态）不在乎了，直接清空影响，同时也需要更新门帮助它实现记忆的更新。更新门更多是用于处理梯度消失问题，可以选择一定程度地保留记忆，防止梯度消失。

重置门影响的是当前步新的候选隐状态的计算，更新门影响的是当前步隐状态的更新程度。