21-22.Animation
Animation
21.Animation
21.1 Historical Points in Animation

远古时期的壁画,可以连成动图

后来可以通过旋转得到动图

第一步手绘的完整动画

里程碑式作品

第一个纯计算机渲染的动画,当时还用的是光栅化
21.2 Keyfram Animation

最早由艺术家绘制关键帧,由助手补上中间的帧
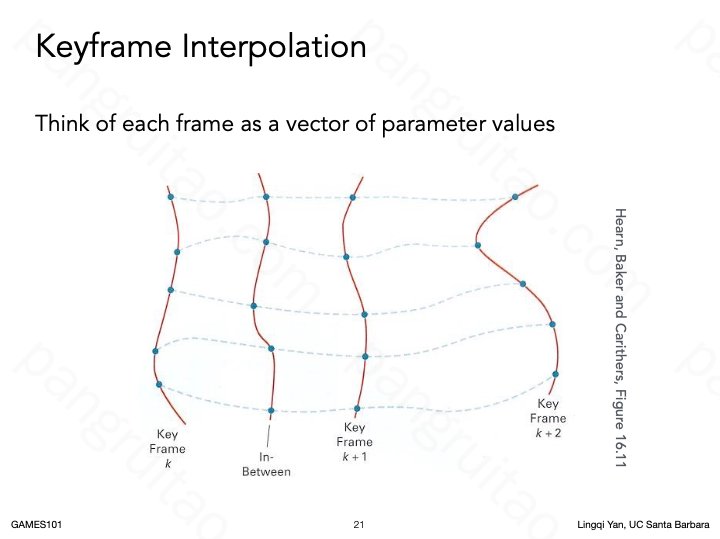
关键帧插值
21.3 Physical Simulation
而现在的动画制作,为了更好的效果往往需要模拟或者仿真
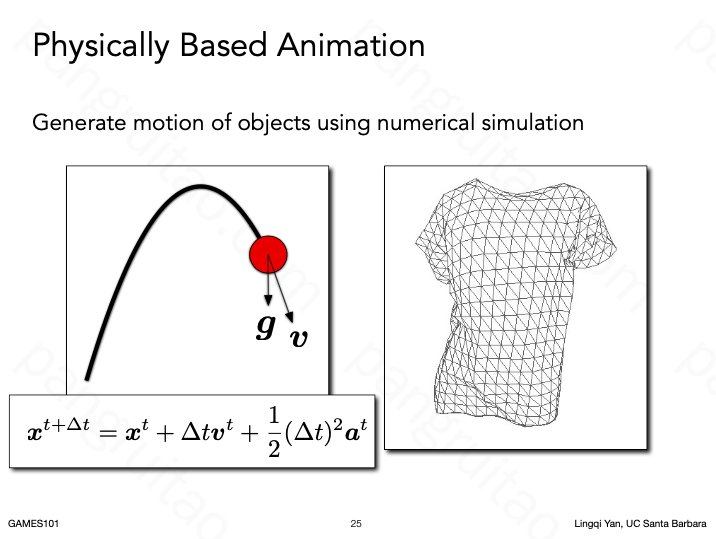

布料仿真

流体仿真
21.4 Mass Spring System

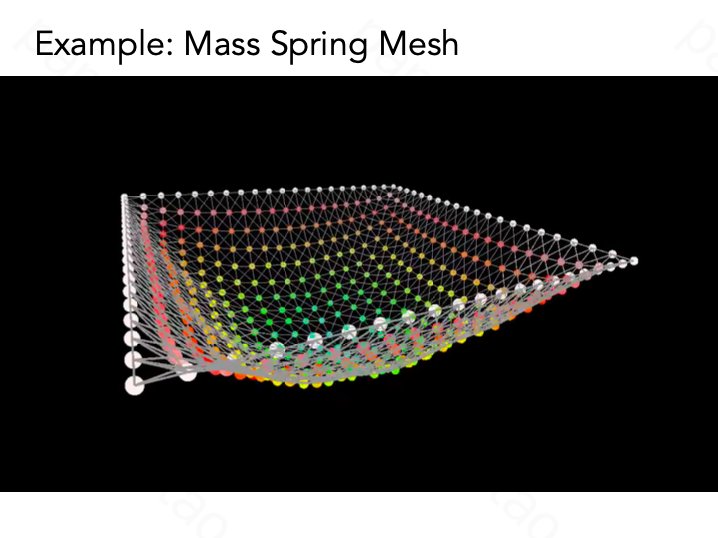

模拟的布料,建模得足够好之后非常接近真实效果

一个简单的质点弹簧模型

带静态长度的弹簧

带能量损失的弹簧,摩擦力与质点速度相反

增加与相对速度相反的摩擦力的模型
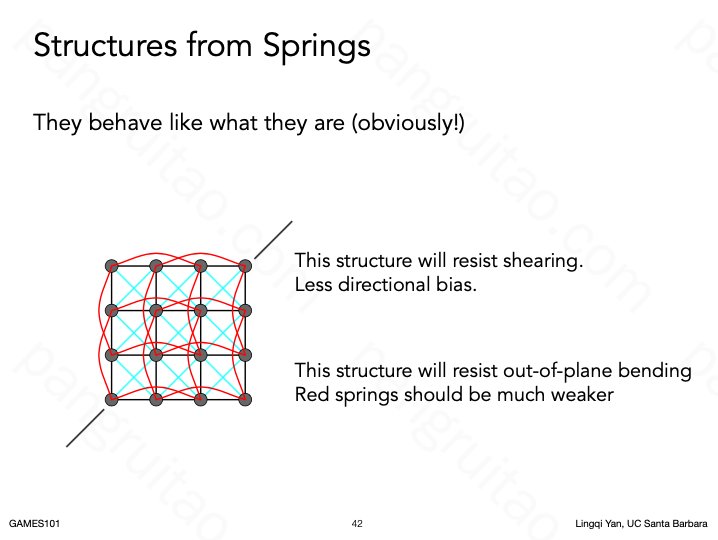
通常用的质点弹簧系统的模型,同时考虑很多性质
- 多个角度牵拉
- 弯折

也可以用有限元方法建模和仿真,可以替代弹簧系统
21.5 Particle Systems

有些东西不太适合有限元或者质点弹簧系统
但可以利用粒子系统,并模拟粒子间的作用(碰撞、引力等等)

粒子系统模拟的粗略过程

粒子系统的一些力

粒子系统模拟水
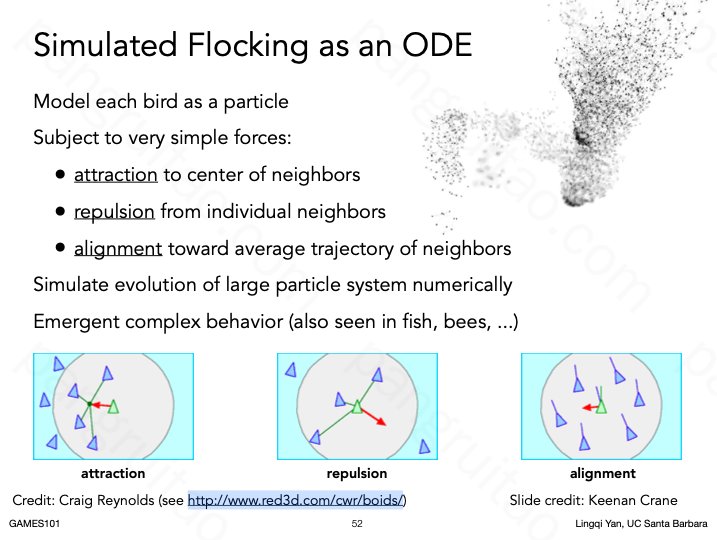
粒子系统模拟鸟群
给每只鸟定义其运动模式,合起来即可模拟鸟群
21.6 Forward Kinematics
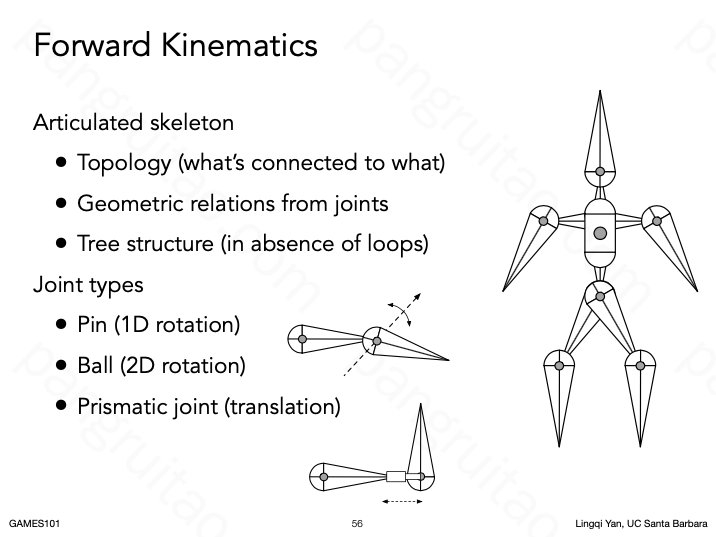
正向运动学是定义模型并操作模型运动
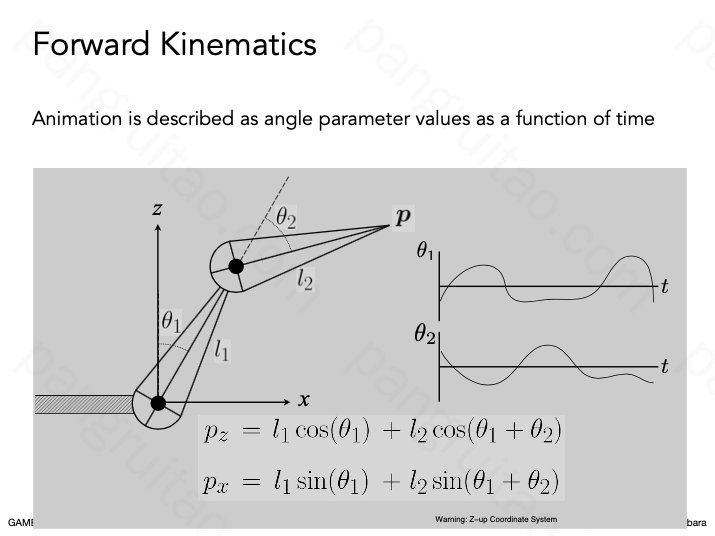
只要从根依次运算即可

坏处是艺术家们并不太方便使用这种不直观的设置方式,更喜欢能够直接拖拽的控制
21.7 Inverse Kinematics
于是有了逆运动学
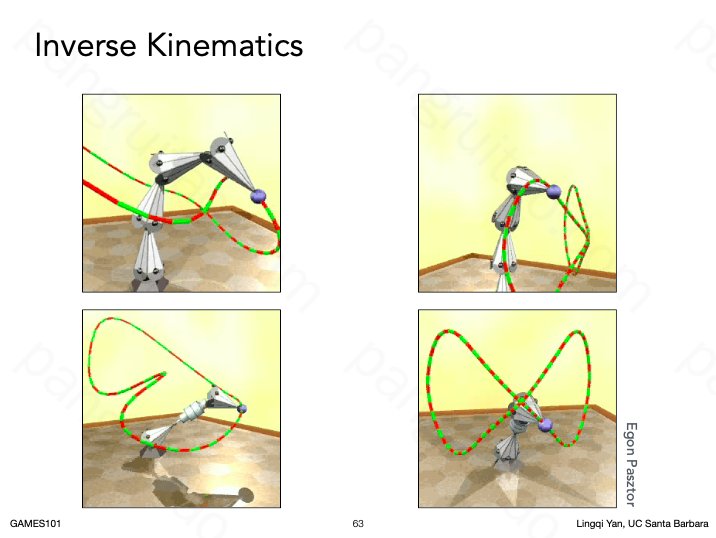
比如设定好想要的轨迹,自动反解出各个关节应该在的地方

两个关节的反解例子
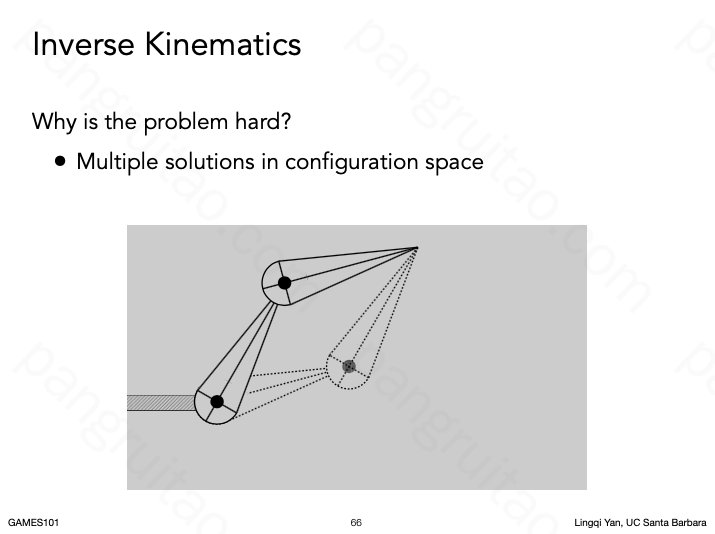
但由于解往往并不惟一,容易导致抖动,这是求解比较难的原因之一
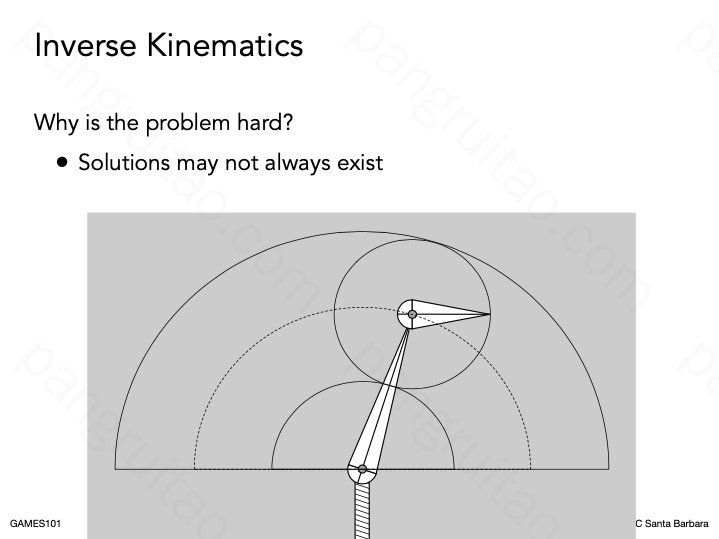
并且,有的时候还可能并不存在解

通常的求解方法类似机器学习,定义误差矩阵,采用梯度下降
21.8 Rigging

设置控制点进行控制


模型插值,可以利用控制点进行插值
21.9 Motion Capture


运动捕捉的优劣

为了让捕捉尽可能全面,遮挡少,可能需要大量摄像机并配合图像识别

面部动画的一大问题
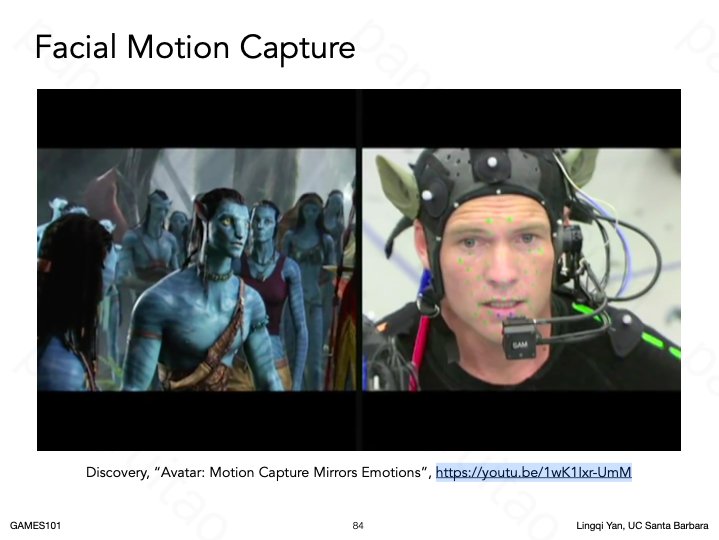
面部表情捕捉
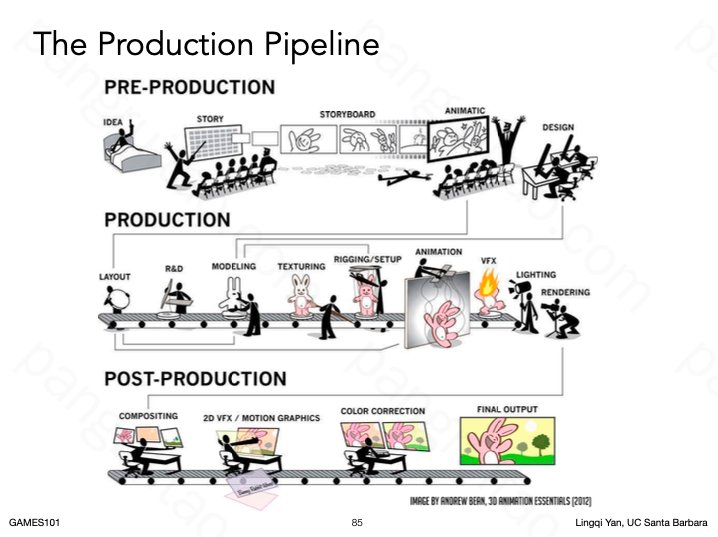
工业界动画制作流程
22.Animation
22.1 Single Particle Simulation
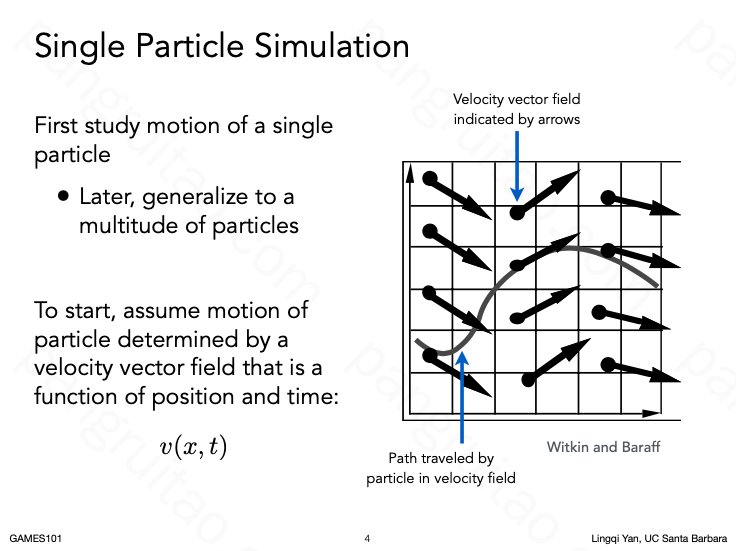
模拟粒子在力场中的运动
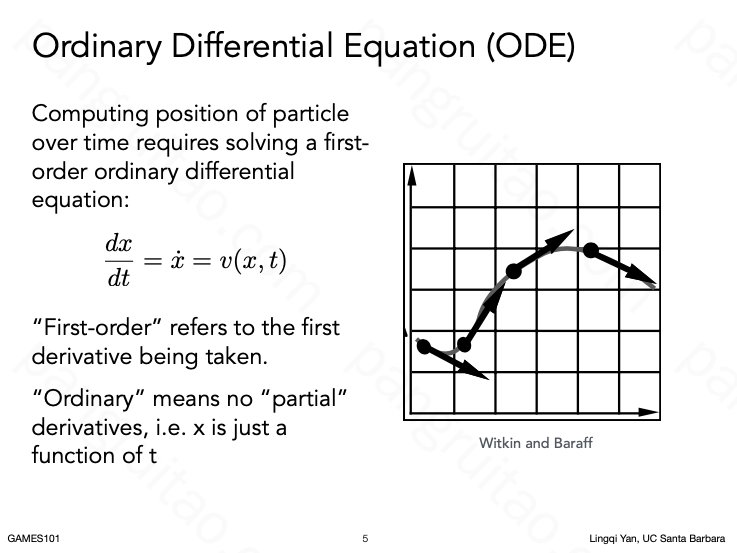
容易想到的方式是用微分方程
但微分方程往往难以求解析解

于是通常需要用差分的方式去模拟,即欧拉方法
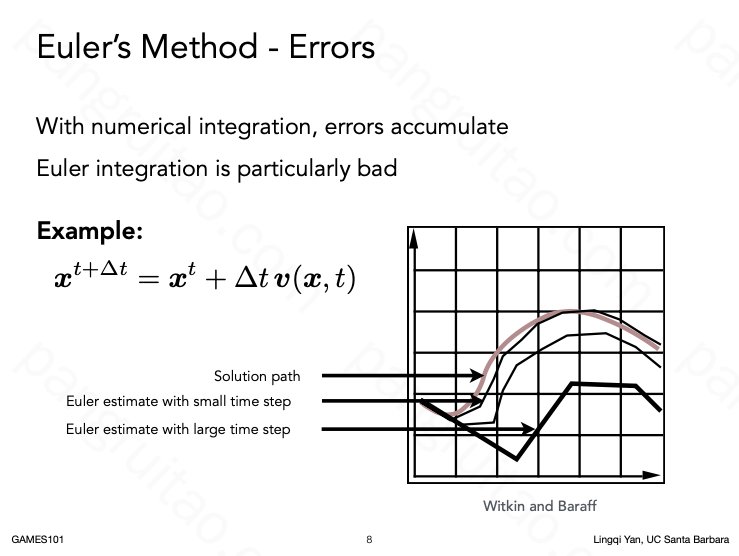
但这样做往往类似三体问题,导致很大误差
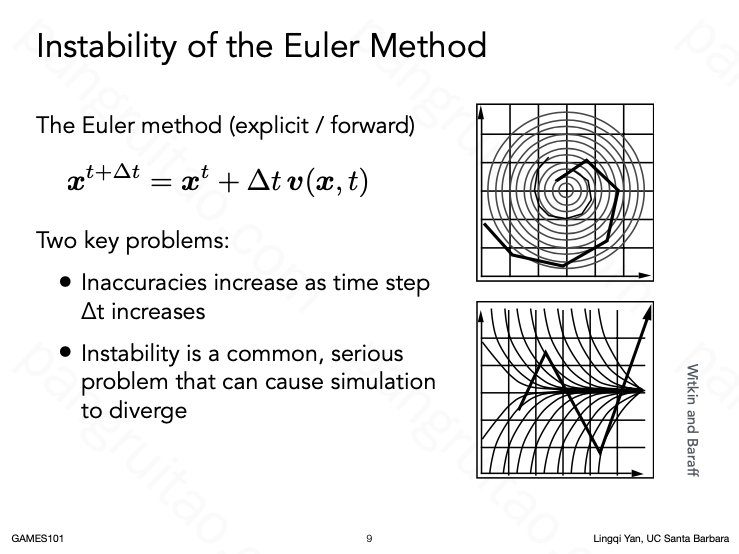
甚至是会导致模式上都非常偏离真实解的误差

数值模拟求解导致的误差和不稳定性
22.2 Combating Instability

一些提升欧拉方法稳定性的方法
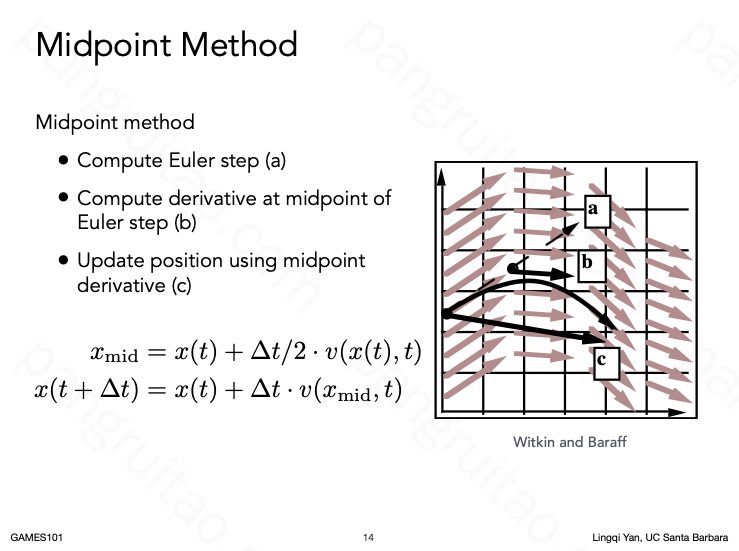
比如可以每次先用欧拉方法计算下一个位置,但并不直接用下一个位置,而是取当前和下一个位置的中点,用中点的力去计算最后用的下一个位置。

另一种方式是类似泰勒展开一般,多利用一个二阶导项,以减小误差
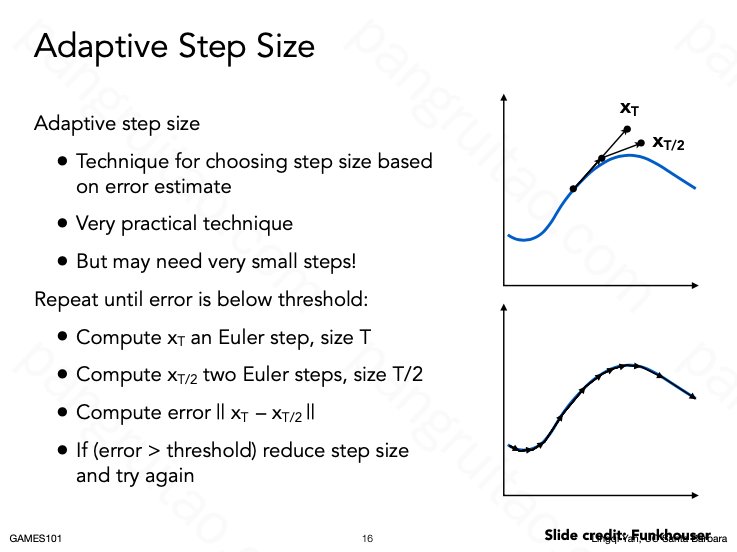
还有一种结合了前面方法的方法,可以设置误差阈值,每次先取中点计算,如果和直接计算的差异足够小则停止,否则继续砍半计算。
这种自适应性在计算和结果稳定性上获得了很好的平衡,效果比较好。

还有一种隐式欧拉法。需要求解方程(往往用牛顿法)

隐式欧拉方法的误差是 𝑂(ℎ2) 比较小

荣格库塔方法族也是很有效的模拟方式,可以直接使用其迭代方程,方程的推导需要参考《数值分析》课程。

最后一种不基于物理,直接基于位置的一些逻辑去模拟,是相对物理的简化方式,在某些场景下效果已经足够。

刚体的模拟方式,需要考虑位置、朝向、速度、角速度这几个量
22.3 Fluid Simulation

水体基于位置的一种模拟方法。
将水的性质进行一些假设,比如水不可压缩,体积不变。
如果某块区域的的水的密度出现相对于静态时的变化,则做相反的调整。

两种对待大量颗粒的方式:
- 拉格朗日法:把每个质点看作独立个体,定义性质,进行模拟
- 欧拉法:把质点们当作整体,考虑各区域的性质,进行模拟

拉格朗日和欧拉法也可以结合起来应用
