10-12.Geometry
10.Geometry:Introduction
由于图形学表现的对象,总需要用几何方法表示或者记录以及检索。所以相关几何知识是必要的。

一个复杂的描述对象的例子
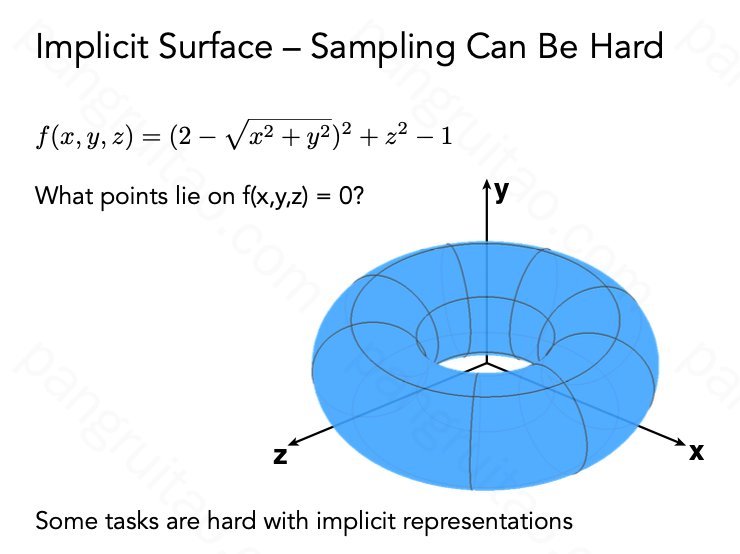
几何的隐式表示:
- 方便查询和检查
- 不方便遍历
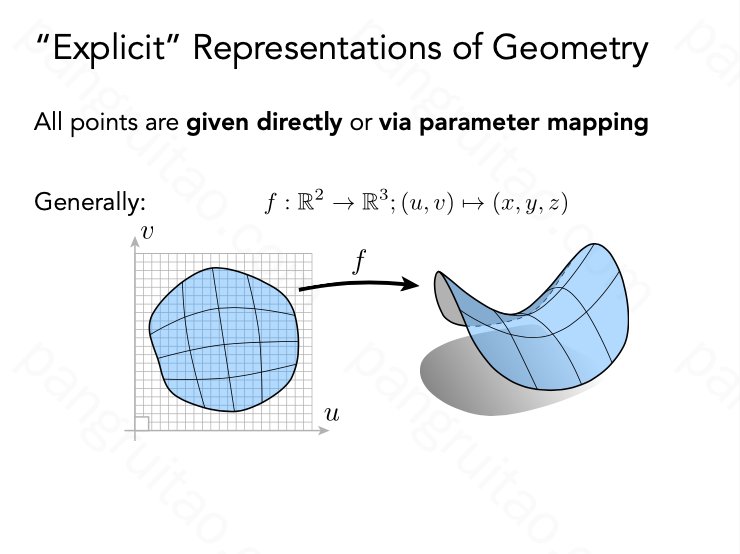
几何的显式表示
- 方便遍历、采样
- 不方便查询


通过布尔运算组合出复杂形状

通过距离函数定义几何表面
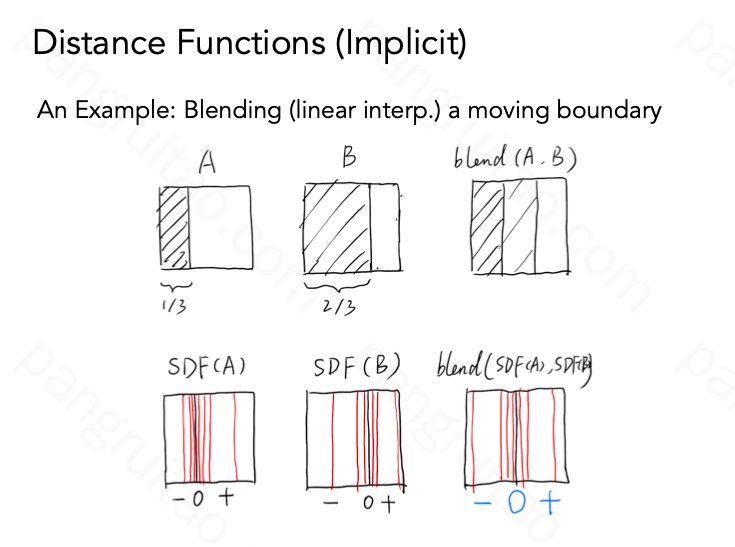
距离函数的定义方法
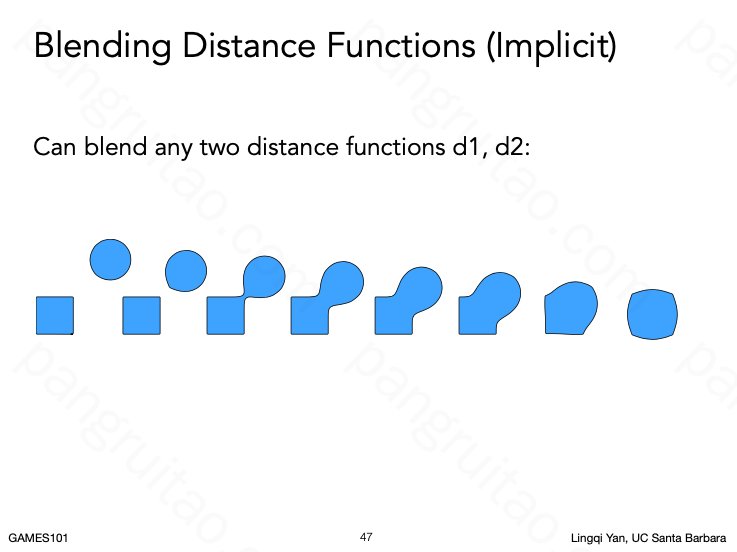
用距离函数进行组合粘连
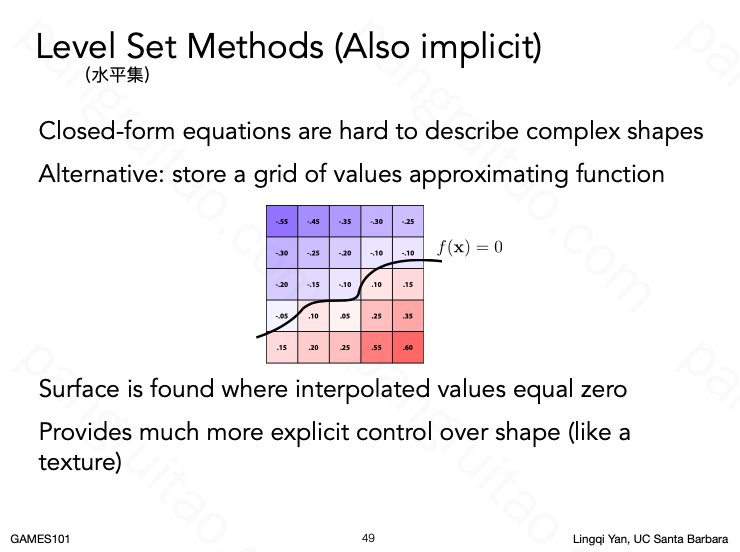
水平集隐式描述
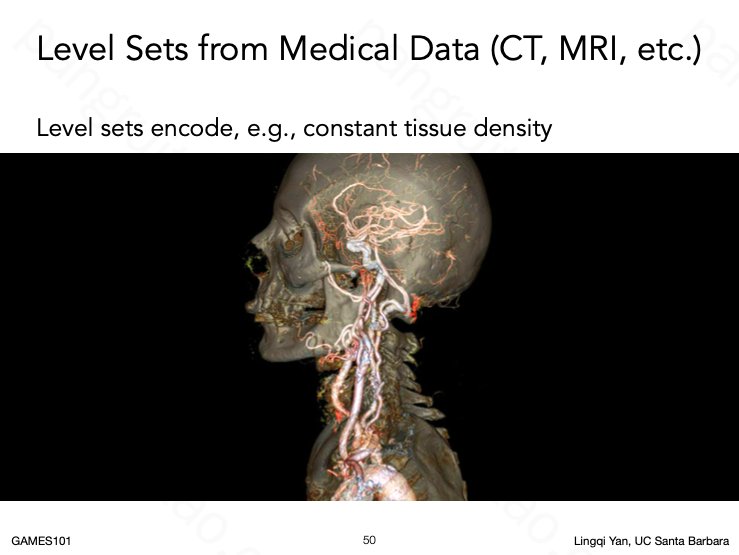
用水平集存储医学数据
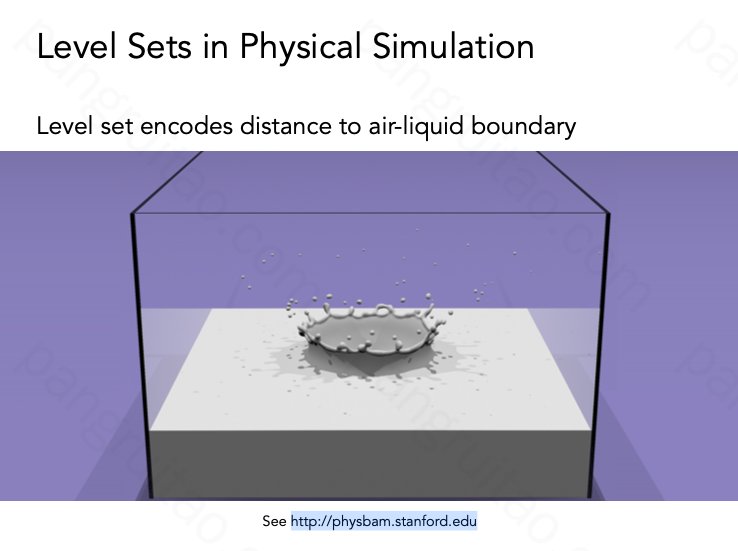
利用水平集进行物理模拟

分型

隐式表示的优劣
11.Geometry:Curves and surface
11.1 简介

通过 Mesh 定义表面
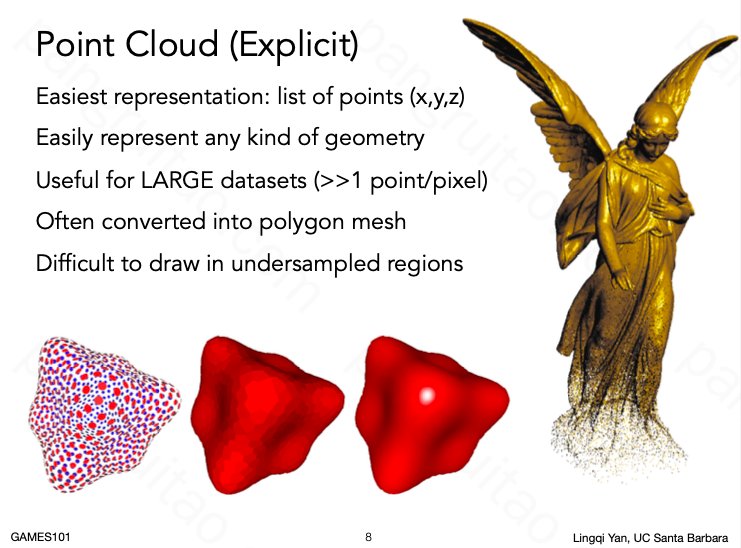
用点云定义物体

常用的 Mesh 文件格式 .obj
例子中定义了一个正立方体
- v 是其各个顶点的坐标
- vn 是其各个面的法线方向(理应只有 6 个面,但由于计算机生成时的精度问题,偶尔会多生成一些)
- vt 记录一些纹理坐标
- f 记录三角形关系,其格式为:
- 第一个顶点的顶点序号/第一个顶点的法线序号/第一个顶点的纹理坐标序号[空格]第二个顶点的顶点序号/…
而对于线条,还可能会在动画运动中有用处

也在矢量图中有应用
11.2 贝塞尔曲线
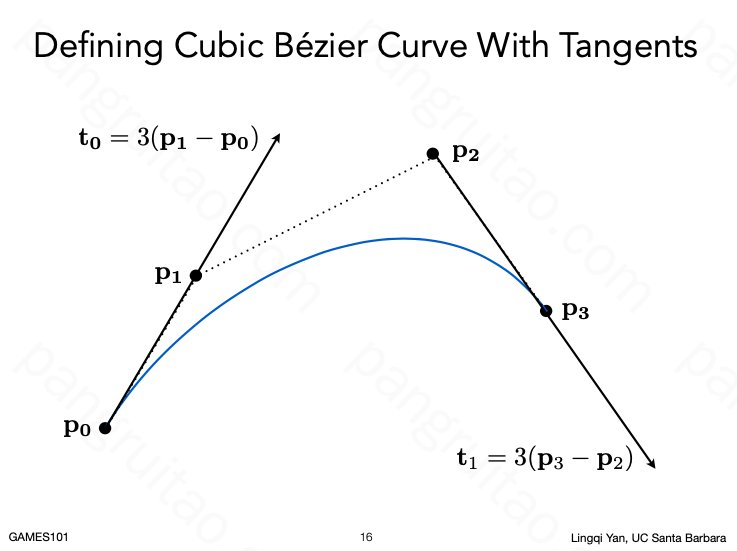
贝塞尔曲线的定义:
- 会经过起点后终点两个控制点
- 起点的速度和起点与第二个点的连线同向,大小成正比
- 终点的速度和倒数第二个点与终点的连线同向,大小成正比
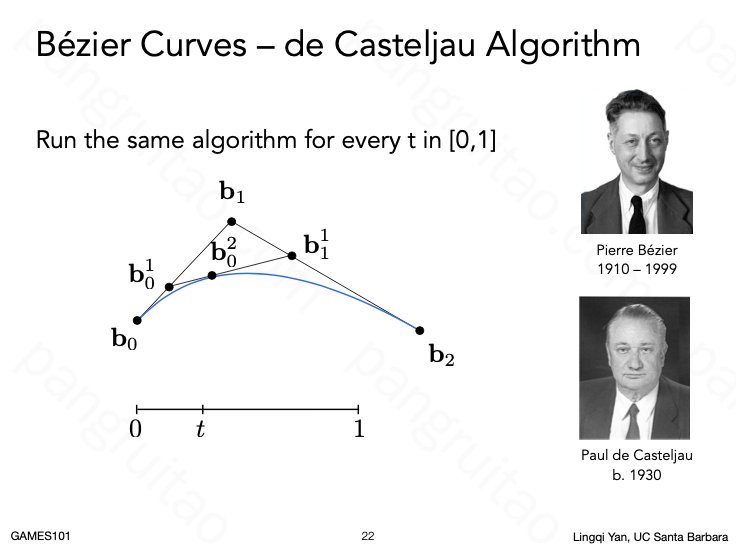
二次(三个控制点)贝塞尔曲线的一种显式画法

三次(四个控制点)贝塞尔曲线的一种显式画法

任意次的贝塞尔曲线画法

贝塞尔曲线的一些性质,特别是有包围盒性质:曲线一定位于控制点所在的凸多边形内
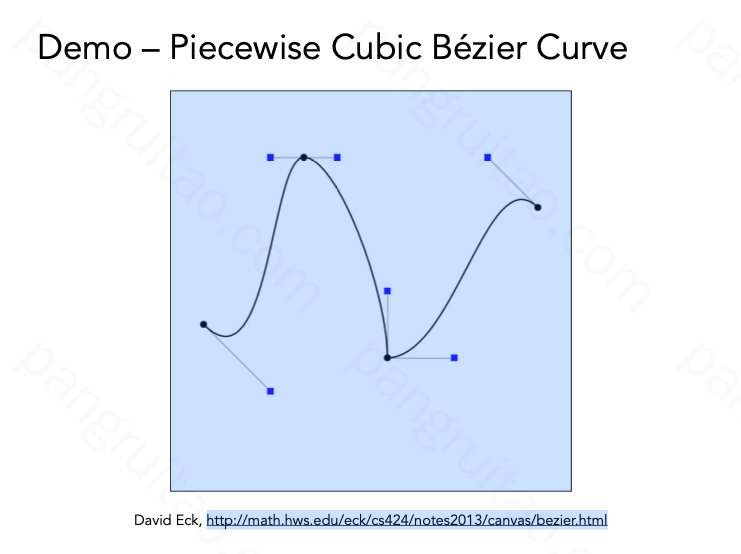
多个贝塞尔曲线相连
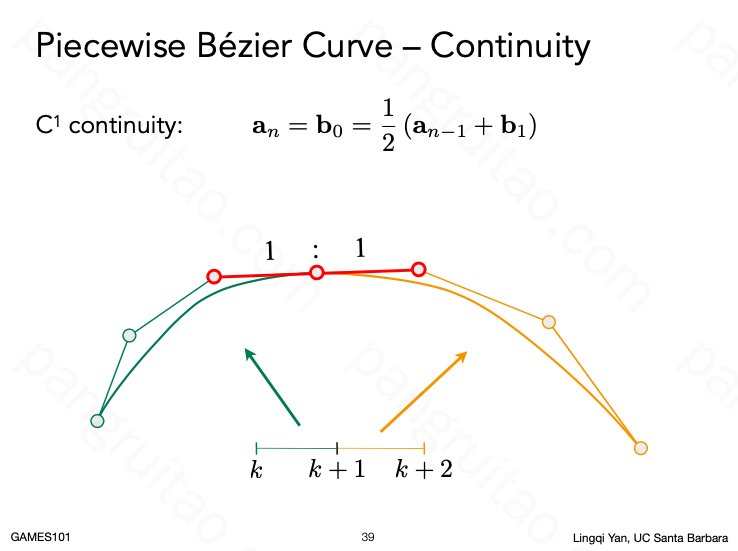
𝐶1 连续,即函数连续、且导数连续

其他类型的线条:Spline,会通过控制点且固定阶导数连续

B 样条
11.3 贝塞尔曲面



相当于对点阵,基于行(或列)先计算一个方向的贝塞尔曲线,再基于计算出的几条曲线从列(或行)再计算一个贝塞尔曲线。
两次即可得到一个贝塞尔平面。
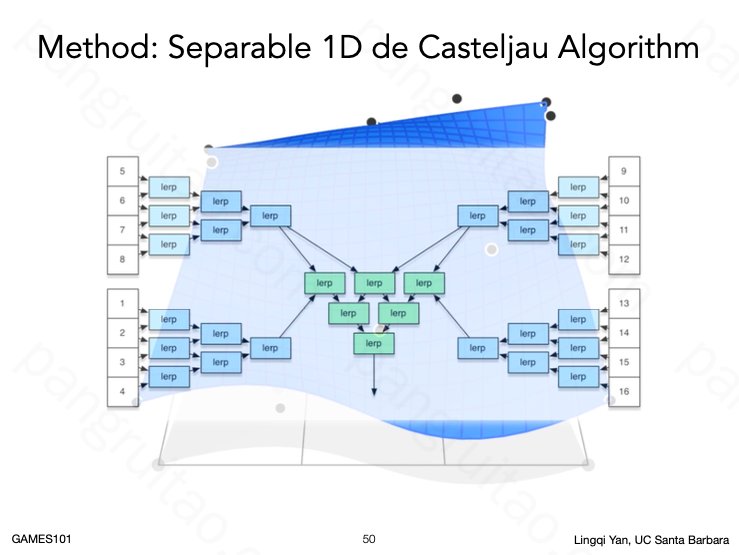
具体的 16 个点的贝塞尔曲线插值计算方式。
12.Geometry:Others
介绍自动升降面数和正规化模型的算法
12.1 Subdivision
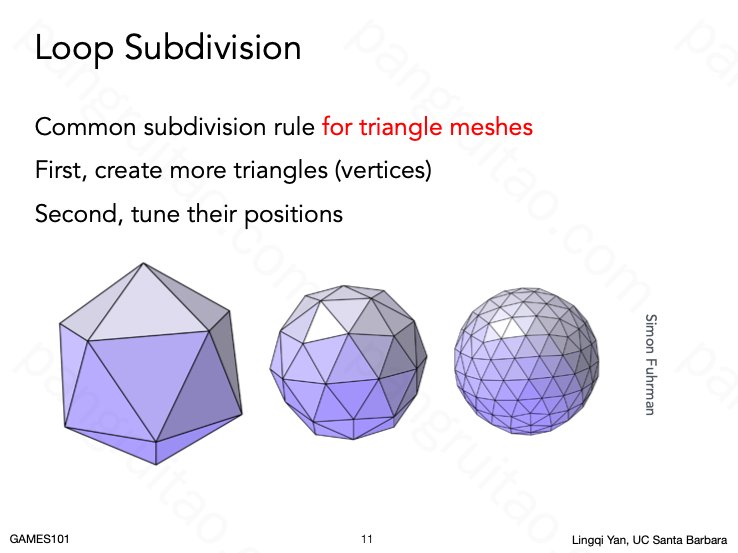
LOOP(名称,不是循环的意思)细分的方法。
简单而言分为两步:
- 创建更多的三角形
- 调整三角形的顶点位置
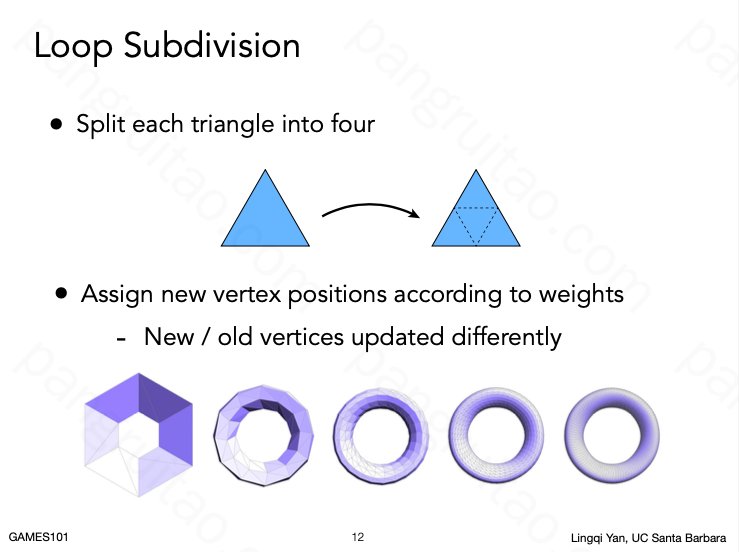
首先基于每个三角形的边中点,将任一三角形细分为四个。
但仅仅细分三角形是不会在视觉上产生差异的。
需要再调整各个顶点的位置。
对新的顶点和老的顶点的位置更新算法略有不同。
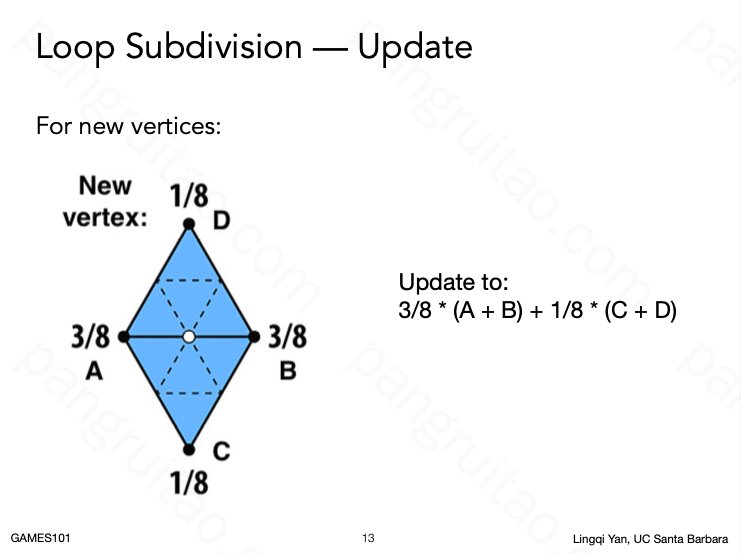
新顶点的调整算法

老顶点的调整算法。看起来会相对复杂一些,但核心思路就是基于自己和与自己相临的其他老顶点的高度进行加权平均。
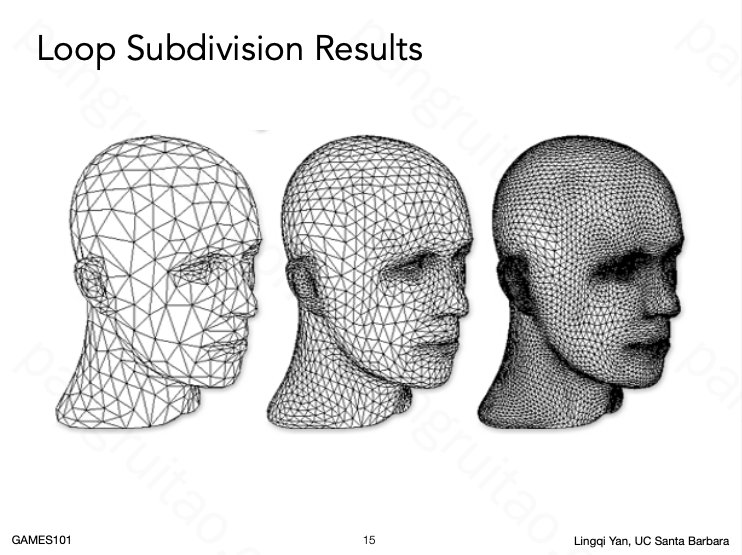
最后达到如上图的细分效果
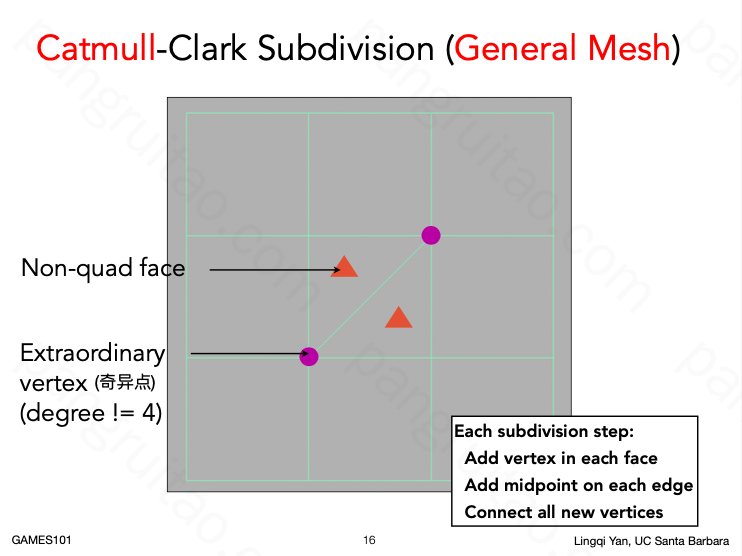
Catmull-Clark 细分,是与 LOOP 细分不同的另一种细分方法。
其主要针对于不全是由三角形构成的 Mesh。
考虑四边形为正常的几何结构。四边形细分非常容易,取中点连线再加权即可。
主要问题是处理三角形结构。
三角形一定会成对出现,有三角形存在的地方一定存在两个度非 4 的顶点。
将顶点根据其度区别为正常顶点和奇异顶点(度非 4 的顶点),奇异顶点一定会成对出现,其连线会将一个四边形划分为两个三角形,此时为这两个三角形每个补充一个顶点(补充的也将是奇异顶点)。
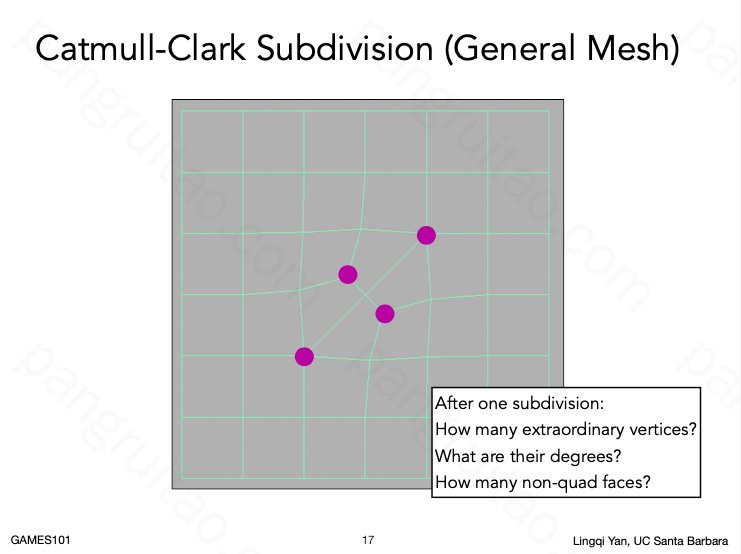
并如图连接,达到细分的效果。
且可以发现,细分之后全部都是四边形,不再存在三角形。但奇异点会继续保持为奇异点。
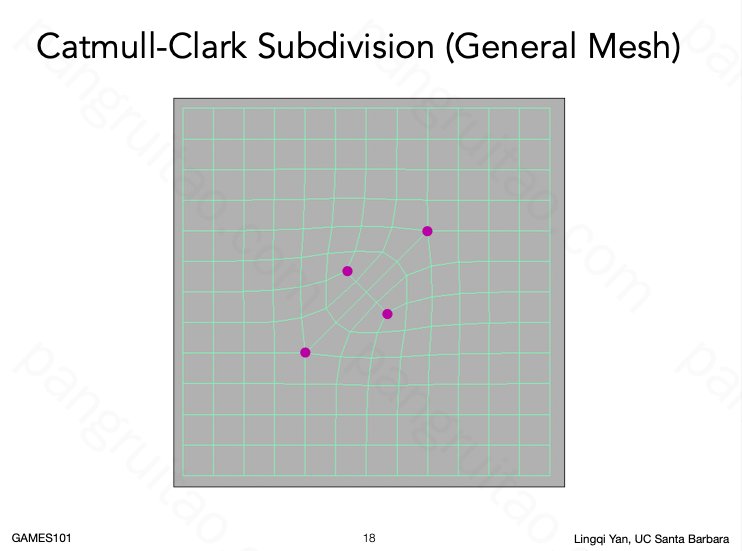
还可以进一步细分下去
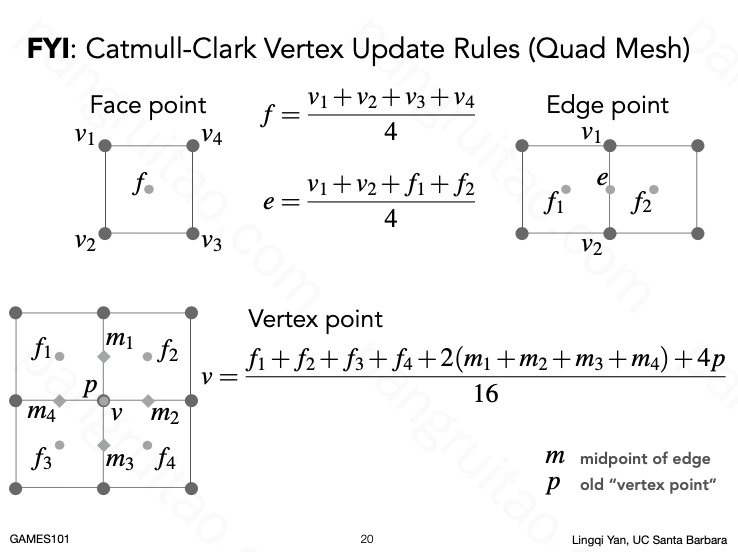
其顶点的更新算法。
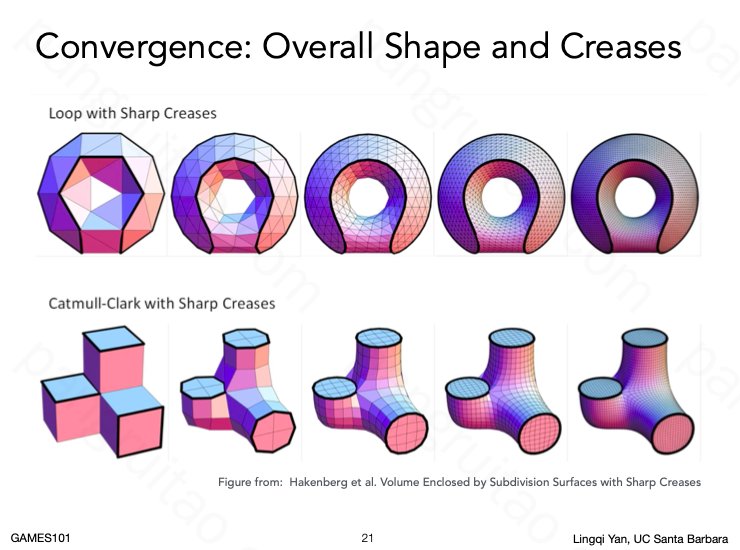
两种算法的效果
12.2 Mesh Simplification
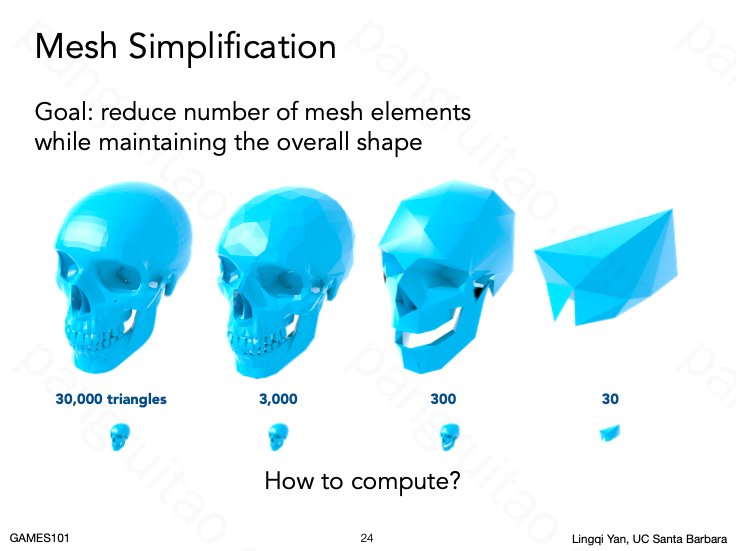
区别于细分,Mesh 简化也是常见的需求。
特别对于游戏,实时渲染需要控制场景的总面数,一种合理的策略是让较远的物体面数偏低,近处的物体面数偏高。
为进一步提升实时性,通常需要同时保存多级模型,即 LOD。分级的过程能自动化则远比手动调整效率高。
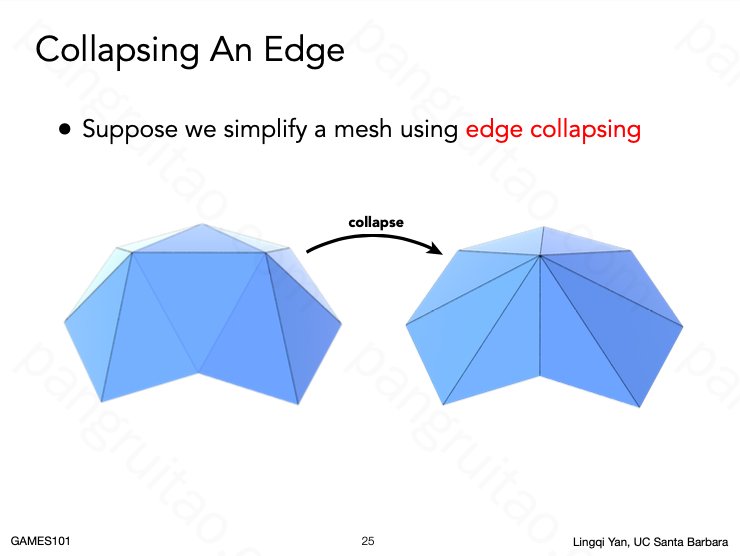
为达到这个目的,边坍缩是一种容易想到的方式。即把相邻的两个点压缩到一起
但实际操作中这个方法并不容易,因为其面临一些隐藏问题:
- 坍缩哪些边?理应优先坍缩不重要的边,但哪些边是不重要的呢?
- 坍缩后的顶点位置也不应该是平均值位置,如图而言讲道理需要高一些,但如何描述呢?

度量贡献度和寻找最小误差的一个方法是二次误差度量法。
核心思路非常类似于线性回归的误差度量。

基于二次误差度量,就可以寻找坍缩代价最小的边,用代价最小的坍缩方式进行坍缩。

基于二次误差度量进行简化的效果
12.3 Shadow Mapping

光栅化由于其局部性问题,想直接实现阴影效果是不行的,需要一些额外的方法。
Shadow Mapping 就是这样的一种普遍的处理方式。不过 Shadow Mapping 只能处理点光源的问题,但对一般的游戏而言通常是足够的。
核心思路是:阴影是那些能直达摄像机,但不能直达光源的像素点。
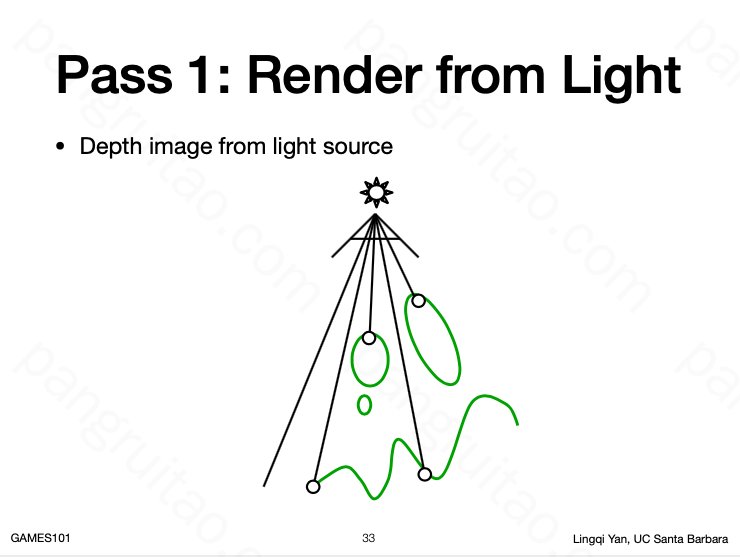
因此,可以首先将摄像机放在光源位置,看看哪些点能被光源直接照亮。
但记录哪些点可以被照亮是一件很难的事情,因为点是可以无限稠密的。
所以一种方式是进行一次深度图渲染。用于保存光源看到的深度信息。
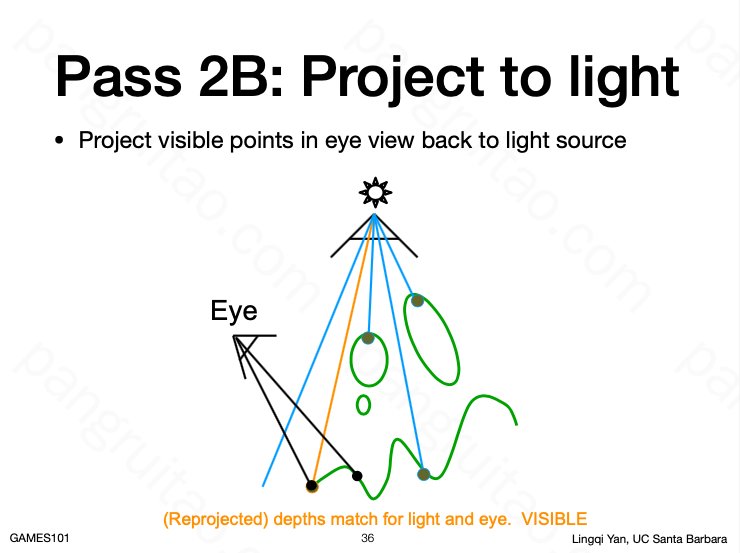
接着,再从眼睛的位置看向场景,渲染每个像素时,计算其在之前光源的深度图中的像素位置,并对比眼睛看到的点的光源深度和之前记录的光源深度。
如果两者深度一致则意味着这个点可以被光源照亮,否则不能被光源照亮。

一个场景的例子
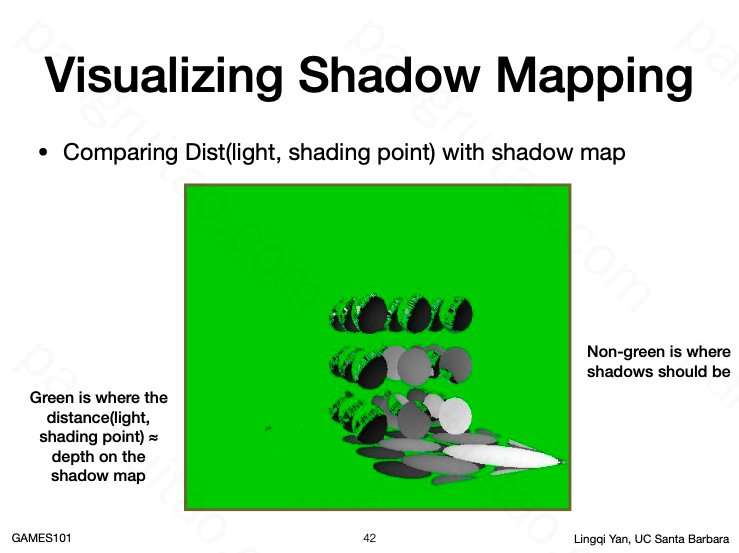
Shadow Mapping 之后的阴影对应的深度图映射在眼睛视角上的效果。


使用 Shadow Mapping 的游戏

但由于 Shadow Mapping 只能处理点光源。于是只能得到硬阴影。而现实世界的光源往往是面光源,因而通常是软阴影,这使 Shadow Mapping 一定程度上不够真实。
要处理这个问题则需要光追算法。
