Rasterization

这节课主要介绍光栅化本身，和现代光栅化的对象–三角形 相关的一些操作。即在经过将场景进行基本变换后，如何将变换后的正方形内容呈现在屏幕上。

介绍成像

首先弄清楚什么是屏幕。 再弄清楚像素，Pixel原来是picture element的浓缩版。

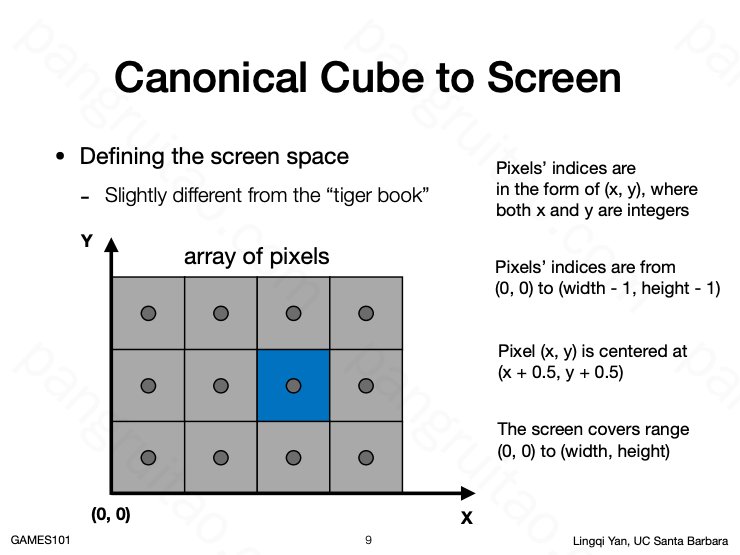
定义屏幕空间，和每个像素的坐标表示方法，此时介绍一下各种成像设备（不仅仅是矩阵式像素成像、甚至不仅仅是屏幕）。

绘制机也算作成像设备，但并非用屏幕，事实上即使用屏幕，也不一定是像素阵列。

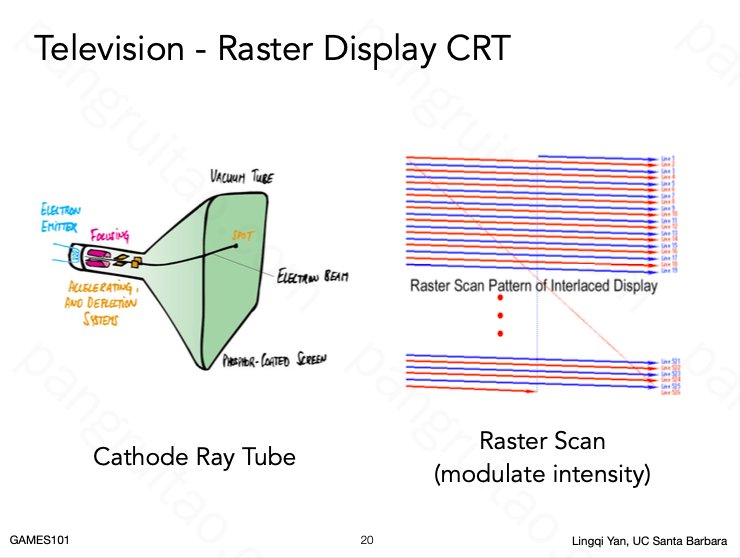
三角形

选用三角形作为基本形体单位的原因。

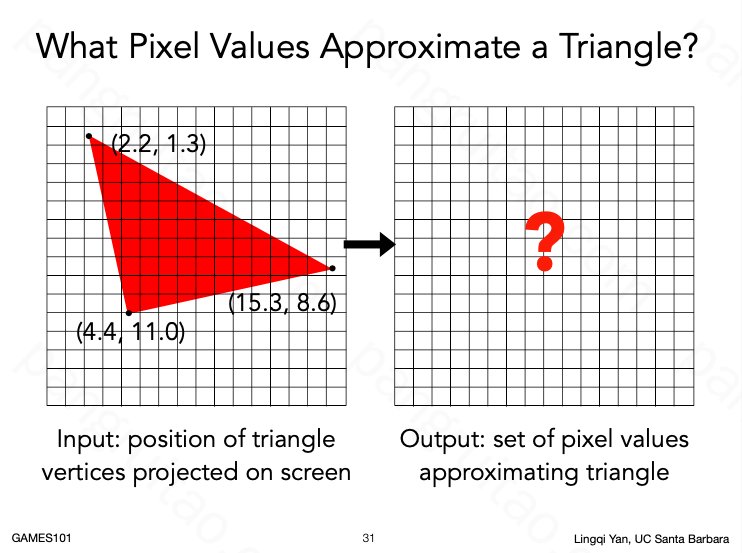
但应该如何把一个三角形给光栅化呢？

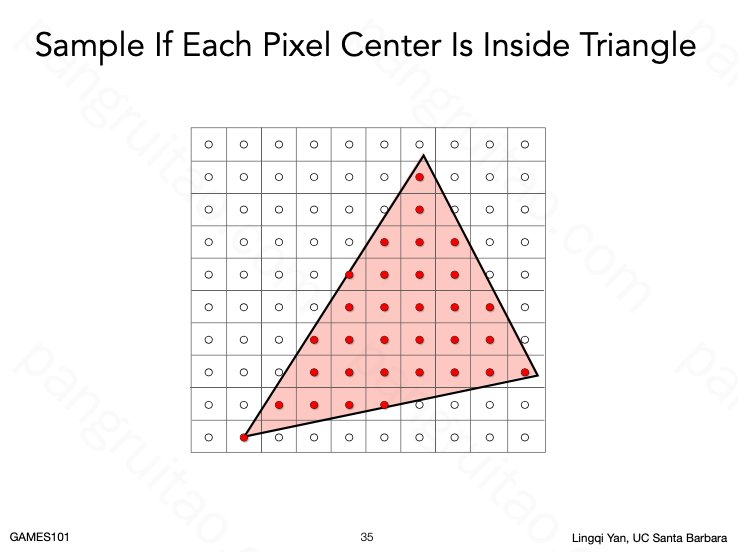
一种方式是对每个像素去采样，中心在三角形内即标内部颜色，否则标外部颜色。判断像素是否在三角形以内可以用叉积判断点是否在三条边（全逆时针或全顺时针）的同侧。同即内部，否则外部。

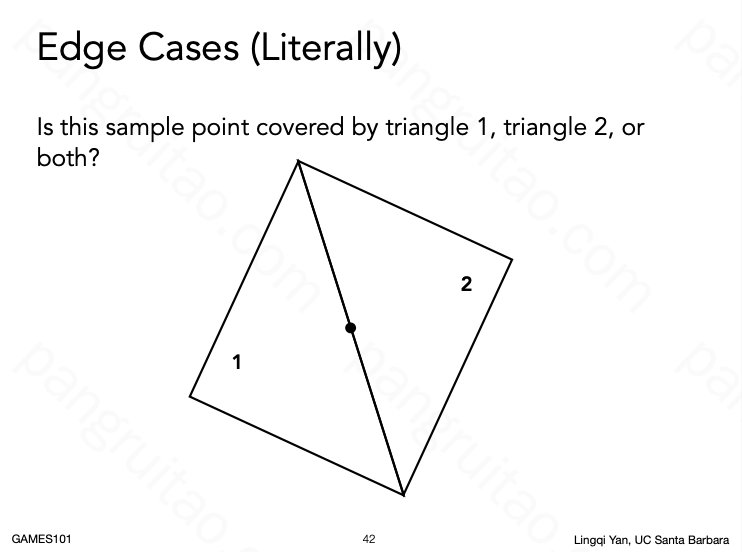
对于刚好在边界的情况，通常只要自己定义清楚就行，在哪边都不会有太大影响（OpenGL会根据是否是左上的边进行区别选择）

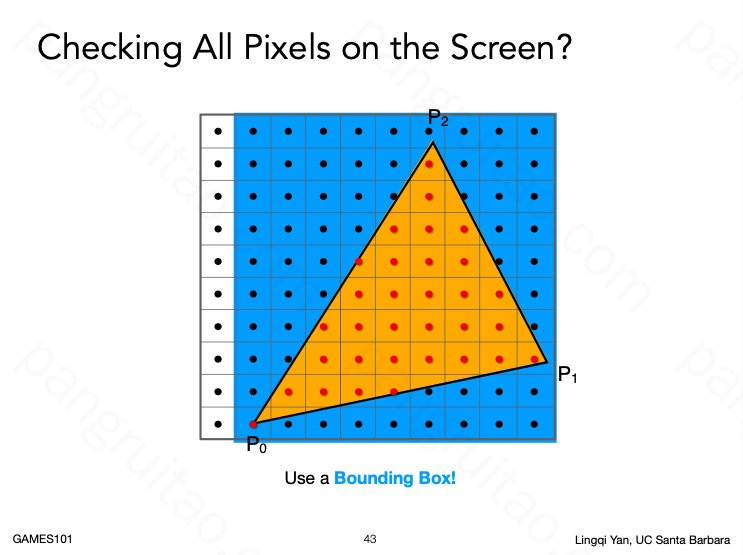
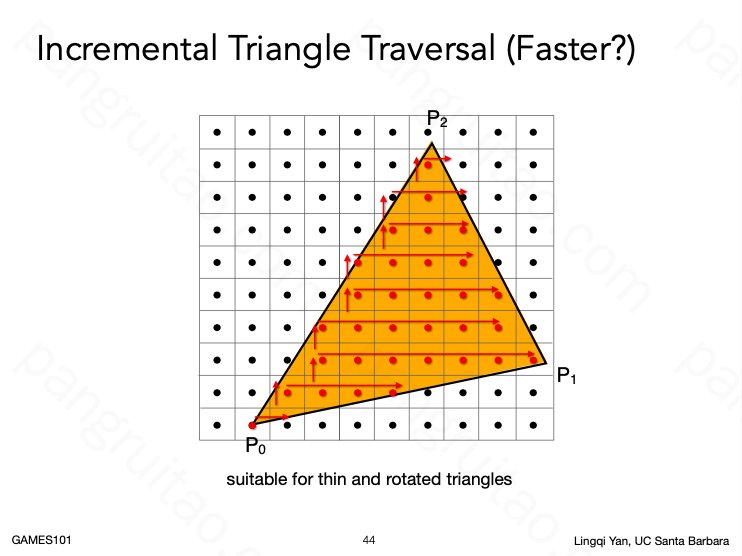
一些加速遍历的方法：

一些实际机器上的像素排列。三星Galaxy S5的排列方式可以节省一些像素点。绿色偏多是由于人眼对绿色更敏感。

一些其他的成像算法。比如打印机用这种排列，目的主要是为了节省油墨。

Antialiasing and Z-buffering

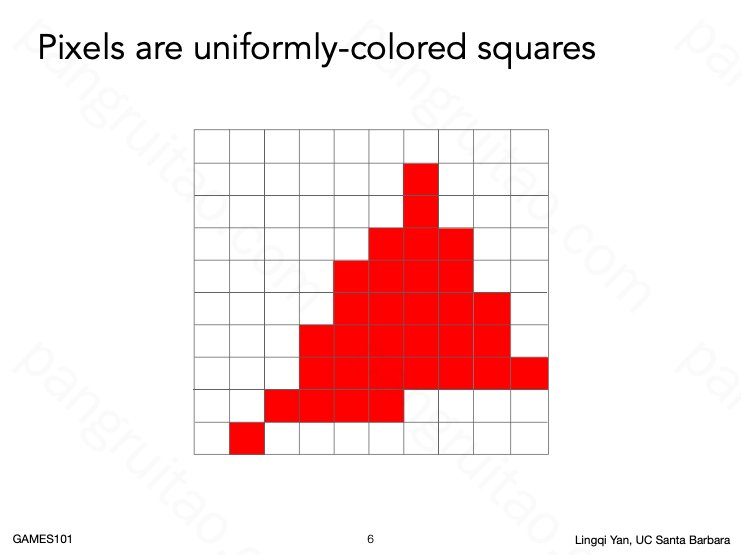
事实上仅仅用上节提到的采样方法，会得到这样的结果。非常不像我们想要的三角形。

甚至还有更严重的事情发生，比如采样得到了完全不同的花纹，这已经不是锯齿的问题了。

还有这种运动错觉（同偶尔看到车轮反转的错觉）这些问题出在哪呢？

都是采样造成的问题，对于其中的锯齿问题：

如果考察照相机（照片一般不会有这种问题），会发现位于边界的每个像素会吸收边界两边的光子，得到一个混合的结果，使整体看上去边界顺滑自然。

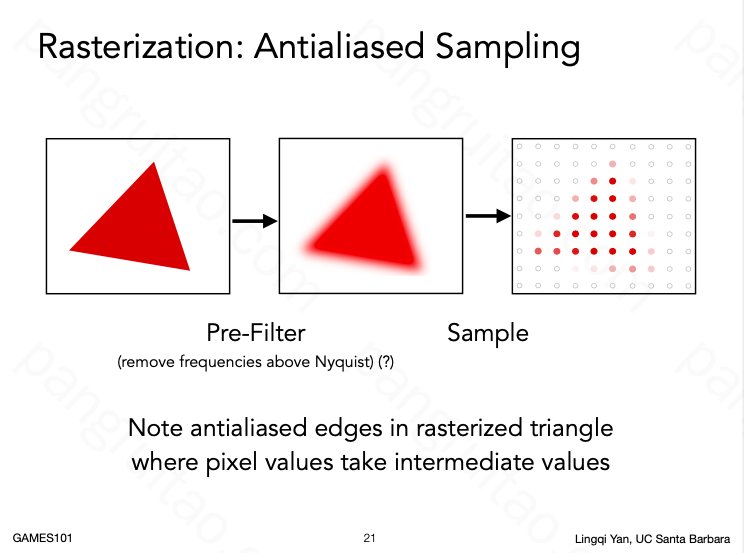
采样时也理应可以做到人工边界模糊，达到接近相机的效果。比如先模糊，再采样。

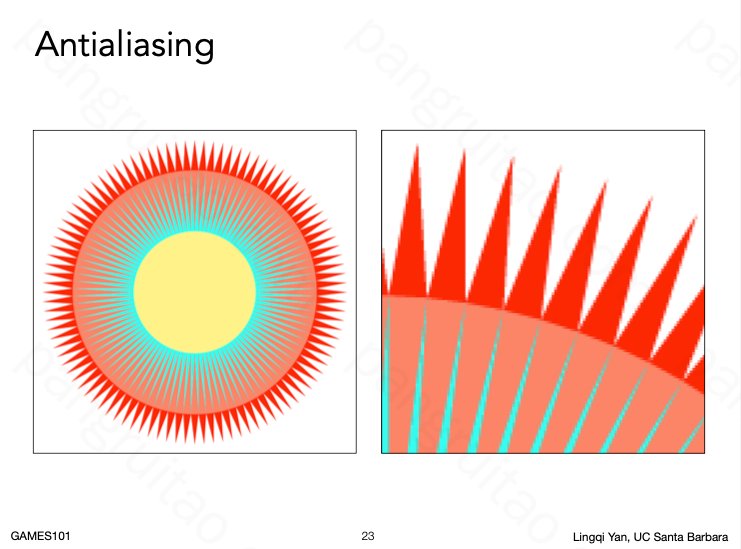
效果还不错：

但做这种事情时需要注意顺序：需要先模糊再采样，而非先采样再模糊。

背后的信号原理

针对于前面的现象，应该如何解释呢？

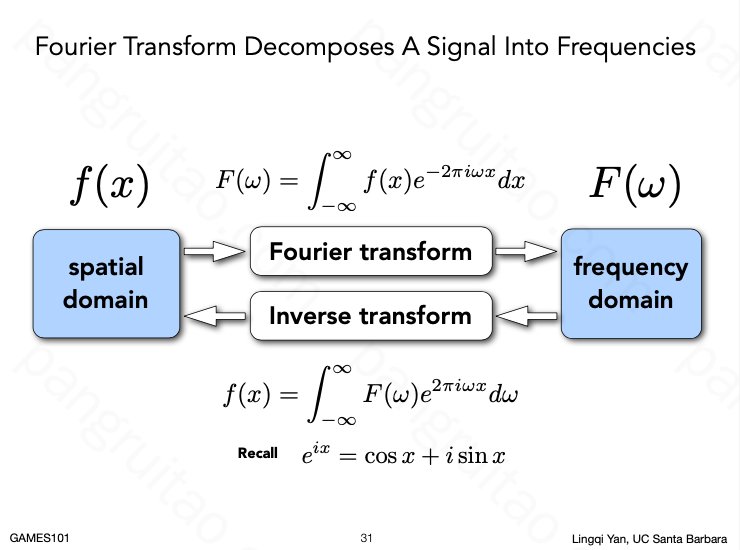
这可以追溯至傅立叶变换：高频信号需要更高的采样率才能保证不失真。

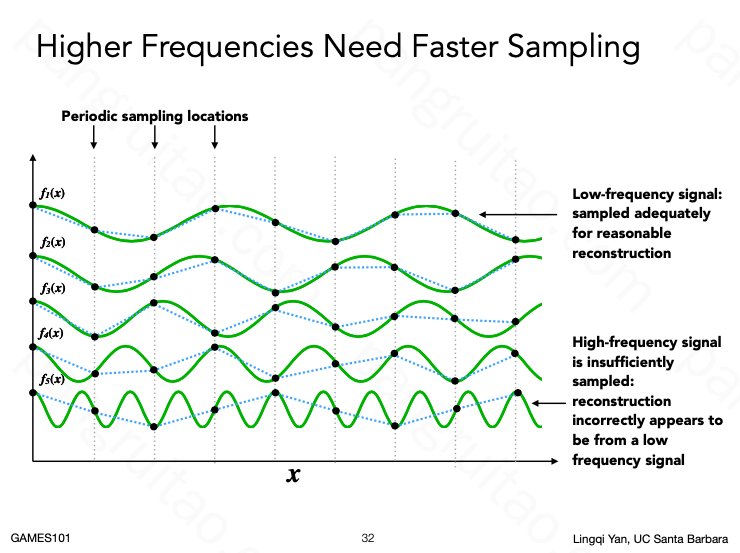
越高频的信号要求越高频的采样，否则会出现走样，对于图片而言，也可以进行二维的傅立叶分解

频域上的两条直线线主要由于做变换时等效于将图片横纵重复了很多次，而边界往往是非常难匹配的，即对应了高频变化。

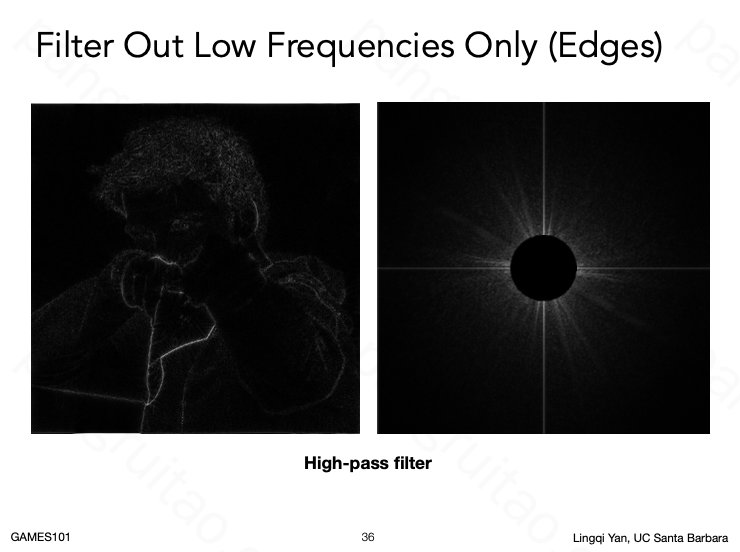
频域上越远离中心，在时域上越对应突变的边：

低频则对应于模糊：

卷积定理：时域上的卷积，对应频域上的乘积。而频域上的卷积，对应时域上的乘积。

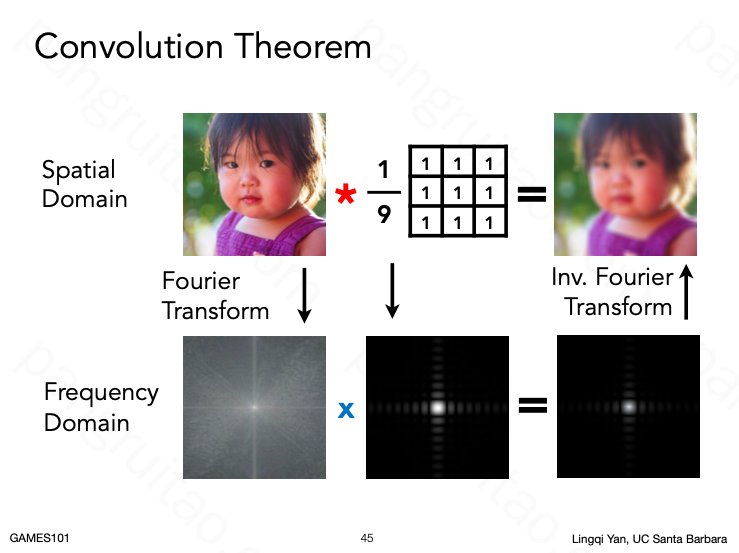
卷积定理的一个例子：

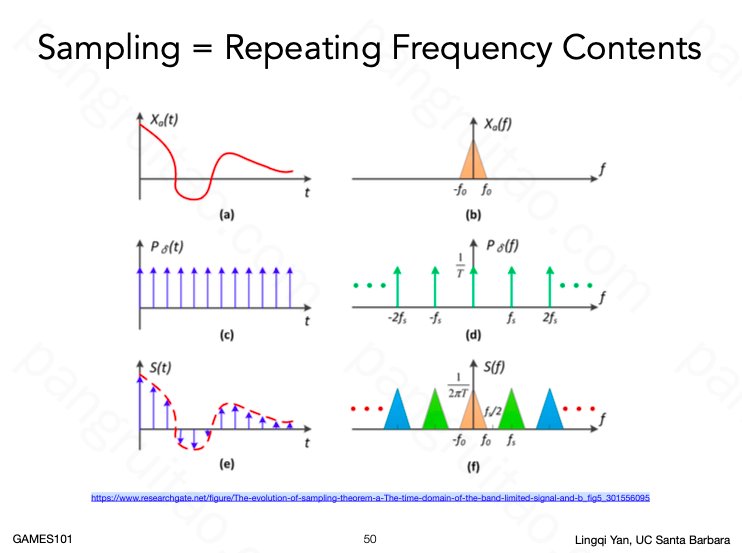
而对于一个时域上的函数a，对其进行固定间隔采样的操作实质等效于用一系列冲击函数c去和a乘，最后得到e。根据卷积定理，时域上的乘积对应频域上的卷积。假设a对应的频域为b。而冲击函数c对应的频域为d。b和d卷积后则理应得到f。

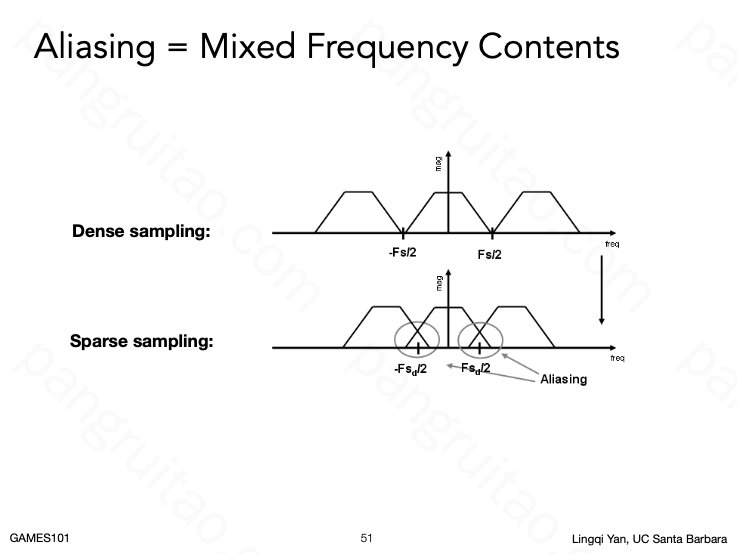
这时我们可以看出如果原始函数比较低频，即对应的频域函数局限在较小区域，则在采样之后不会有重叠。否则，则会在频域上有重叠，进而对于重叠部分无法区分是重叠导致的，还是原始信号天生如此，造成走样。

据此，分析反走样的原理也就比较容易了。要么提高采样频率，相当于增大频域上的间隔，使其不容易重叠。

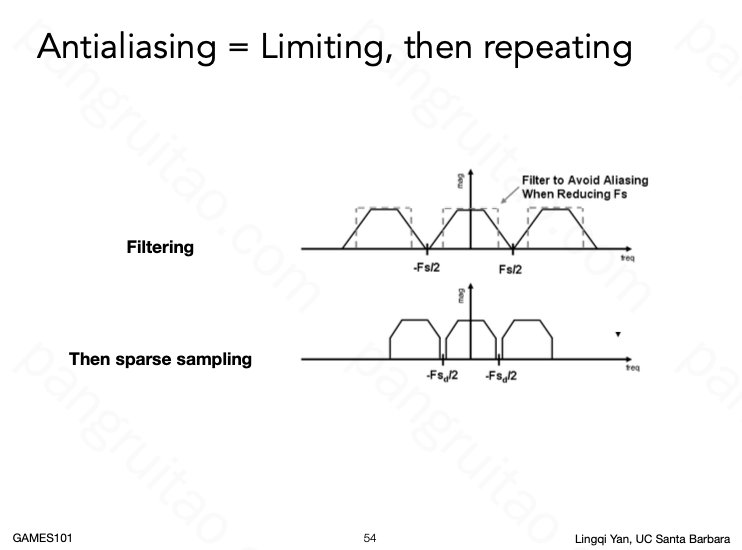
也可以通过模糊化操作，使其不包含高频信号，以至于不会重叠：

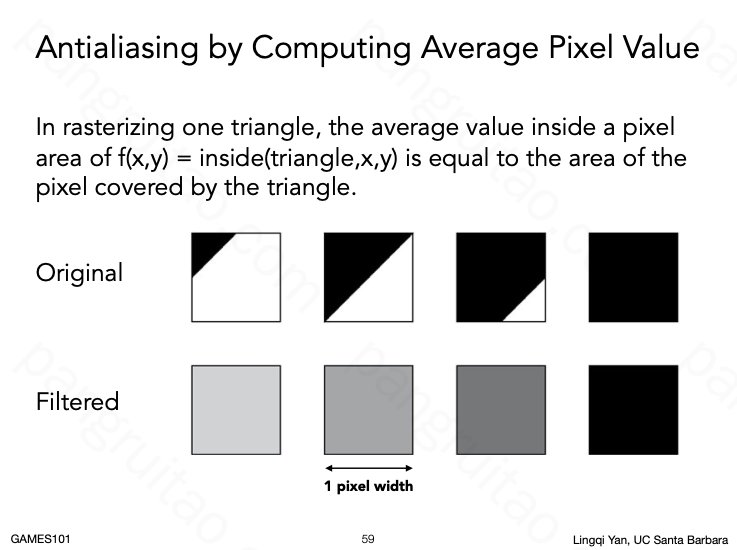
除了模糊化以外，还可以采用对单个像素密集采样求平均的方法来减少锯齿或走样问题。

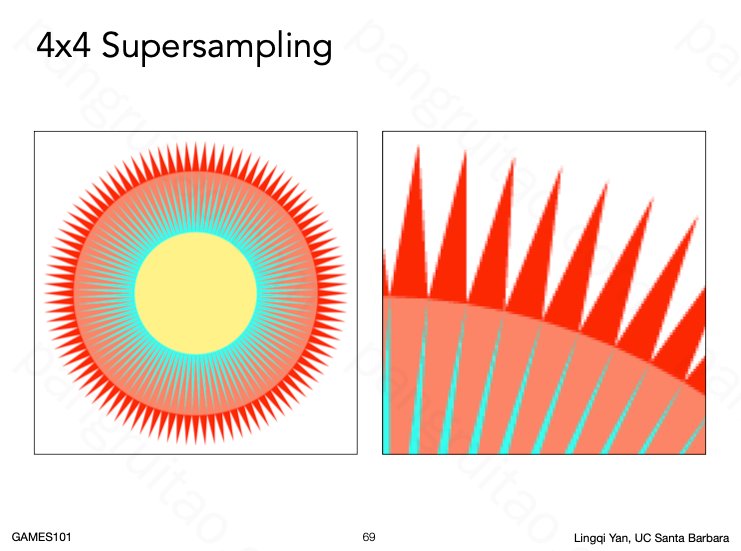
也能达到很好的效果，不过与此同时也需要付出计算代价。

光栅化一个场景

知道了如何光栅化一个三角形，再介绍如何光栅化一个场景。

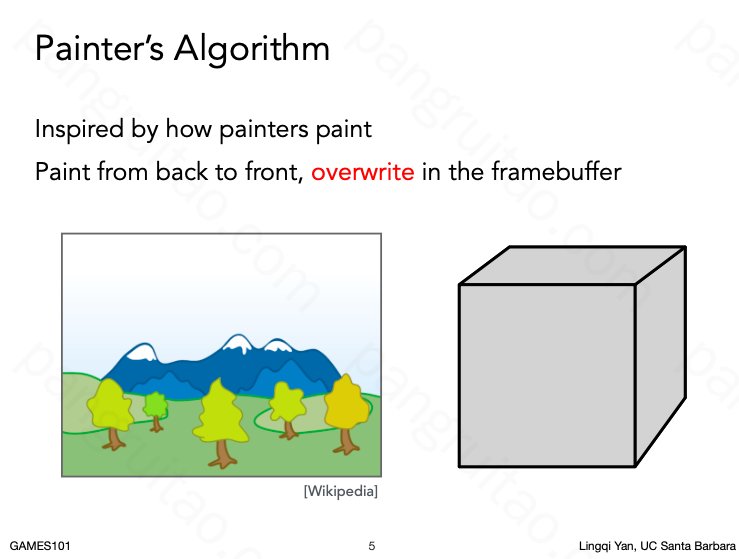
为了解决远近覆盖问题。容易想到的一种处理方式是画家算法：由远往近依次画。画的时候近处物体覆盖远处物体。

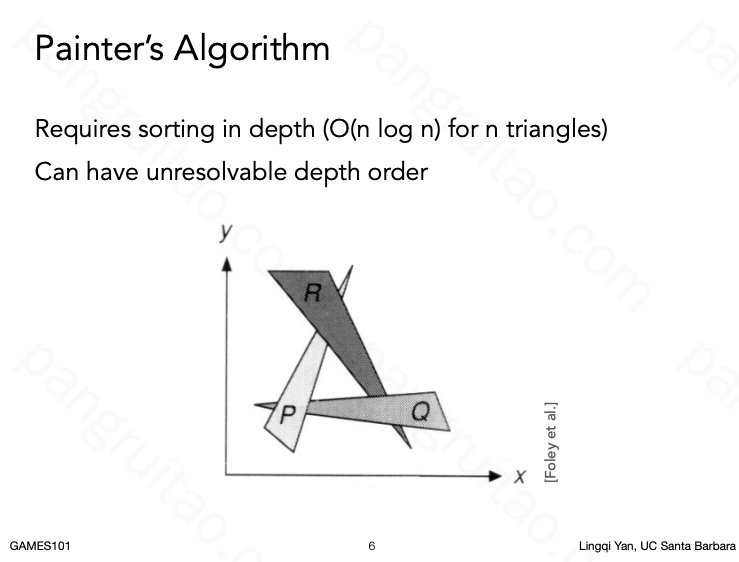
但这样做也是有局限的。特别是有些情况下难以对三角形进行远近排序。

对三角形难以远近排序，对像素却是可以做到的，所以有了Z-Buffer算法。每个像素用Z最近的光栅化值。

实际上等效于在记录RGB三色的同时，加入Depth的记录。

由于只用找最小，而不是排序，所以Z-Buffer复杂度仅 𝑂(𝑛)，且为了更高的运行效率， Z-Buffer已经集成在了各个GPU内部，直接硬件层面支持。