采样与量化

为了用计算机来处理，图像必须用合适的离散数据结构来表达, 例如矩阵。传感器获取的图像是平面上两个坐标的连给函数 $f(x, y)$ 图像数字化是指将 $f(x, y)$ 采样（sampled）为一个 $M$ 行 $N$ 列的矩阵。图像量化（quantization）给每个连续的样本数值一个整数数字，图像函数 $f(x, y)$ 的连续范围被划分为 $K$ 个区间。采样及量化越精细（即，$M, N, K$ 越大)，对连续函数 $f(x, y)$ 的近似就越好。

图像函数采样有两个问题，其一是确定采样的间隔，即相邻两个采样图像点的距离，其二是设置采样点。

采样

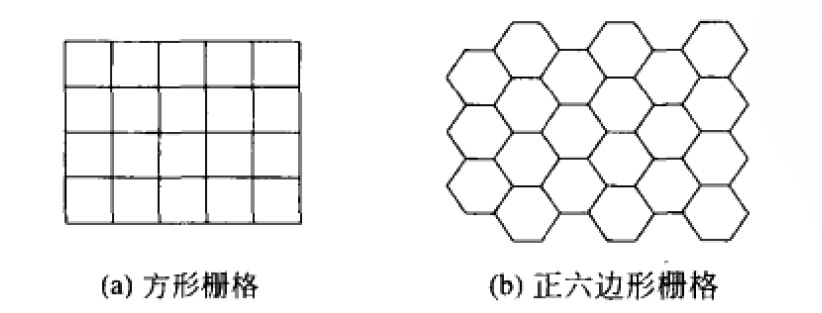
一个连续图像在采样点(sampling point)处被数字化。这些采样点是在平面上排列的，称它们的几何关系为栅格(grid)。因此数字图像是一个数据结构，通常是矩阵。在实践中，栅格一般是方的或者是正六边形的。