图像数字化

图像函数的值对应于图像点的亮度。函数值也可以表示其他物理量(温度、压力分布、离观察者的距离等)。亮度(brightness)集成了不同的光学量,将亮度作为一个基本量使我们得以避免对图像的成像过程进行描述。人类眼睛视网膜或者 TV 摄像传感器上的图像本身是两维的(2D)。我们将这种记录了明亮度信息的 2D 图像称为亮度图像(intensity image)。图像传感器上的 2D 图像通常是三维(3D)场景的投影结果。这一过程的最简单的数学模型就是所谓的针孔摄像机。

2D 亮度图像是 3D 场景的透视投影(perspective projection),这一过程由针孔摄像机拍摄的图像来表达。在下图中,图像平面被相对于 XY 平面反折过来了,以便避免使用具有负坐标的镜像图像;x,y,z 的量是世界坐标系中 3D 场景点 X 的坐标,f 是从针孔到图像平面的距离。通常称 f 为焦距,因为在镜头中它具有相似的含义。镜头近似于针孔摄像机而广为应用。投影后的点 u 具有 2D 图像坐标平面中的坐标$(u,v)$,根据相似三角形很容易导出：

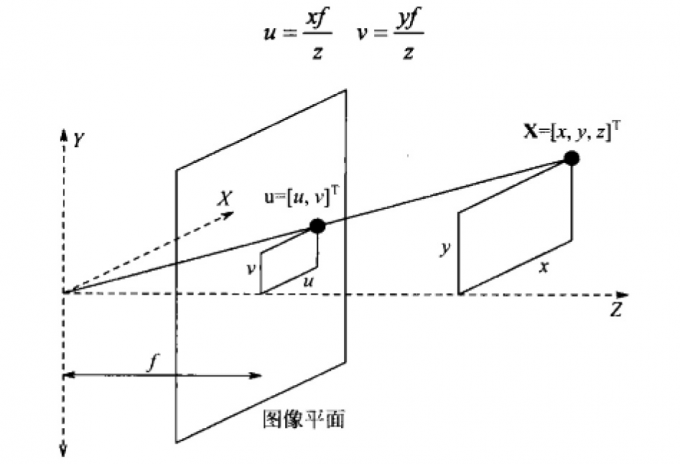
非线性的透视投影常被近似为线性的平行（parallel）（或正交（orthographic）) 投影（projection）, 其 中 $f \rightarrow \infty$ 。隐含地，$z \rightarrow \infty$ 表明正交投影是远处物体透视投影的极限情况。当 3D 物体经透视投影映射到摄像机平面后,由于这样的变换不是一对一的,因而大量的信息消失了通过一幅图像来识别和重构 3D 场景中的体是个病态问题。可以预料,这不是一个简单的任务,涉及到试图建立图像中点的深度( depth)这个中间表达层次。目标是恢复完整的 3D 表达,比如计算机图形学中的表达,即,独立于视点的表达,表示在物体坐标系中而不是在观察者坐标系中。如果这样的表达可以恢复,则物体的任何视角的亮度图像可以用标准的计算机图形学技术合成出来。

图像处理通常考虑的是静态(static)图像,时间 t 作为常量。单色的静态图像是用连续的图像函数 f(x,y) 来表示的,其中的变量是平面的两个坐标。本书所考虑的图像除非特别声明大多数是指单色的静态图像。通常把这里所讲的技术推广到多光谱的情况下是显而易见的。计算机化的图像处理使用的数字图像函数通常表示成矩阵的形式,因此其坐标是整数。图像函数的定义域是平面的一个区域 R：

$$ R=\left{(x, y), 1 \leqslant x \leqslant x_{n}, 1 \leqslant y \leqslant y_{n}\right} $$

其中 $x_m$，$y_n$ 表示最大的图像坐标。图像函数具有有限的域由于假定图像函数在域 R 外的值为零,可以使用无限求和或积分的形式。尽管矩阵中使用的(行、列、左上原点)定位方式在数字图像处理中也常用到,但是习惯上采用的图像坐标方向仍然是普通的笛卡尔形式(横轴 x、纵轴 y、左下原点)图像函数的值域也是有限的,按照惯例,在单色图像中最低值对应于黑,而最高值对应于白。在它们之间的亮度值是灰阶(gray-level)。

数字图像的品质随着空间、频谱、辐射计量、时间分辨率增长而提高。空间分辨率( spatial resolution)是由图像平面上图像采样点间的接近程度确的,频谱分辨率( spectral resolution)是由传感器获得的光线频率带宽决定的,辐射计量分辨率( radiometrie resolution)对应于可区分的灰阶数量,时间分辨率(timeresolution)取决于图像获取的时间采样间隔。时间分辨率问题在动态图像分析中是重要的,其中处理的是图像的时间序列。图像 f(x,y) 可作为确定的函数或者是随机过程的实现来看待。图像描述中的数学工具根植于线性系统理论、积分变换、离散数学以及随机过程理论中。