原文地址 TODO!

渲染管线中的顶点变换

概述

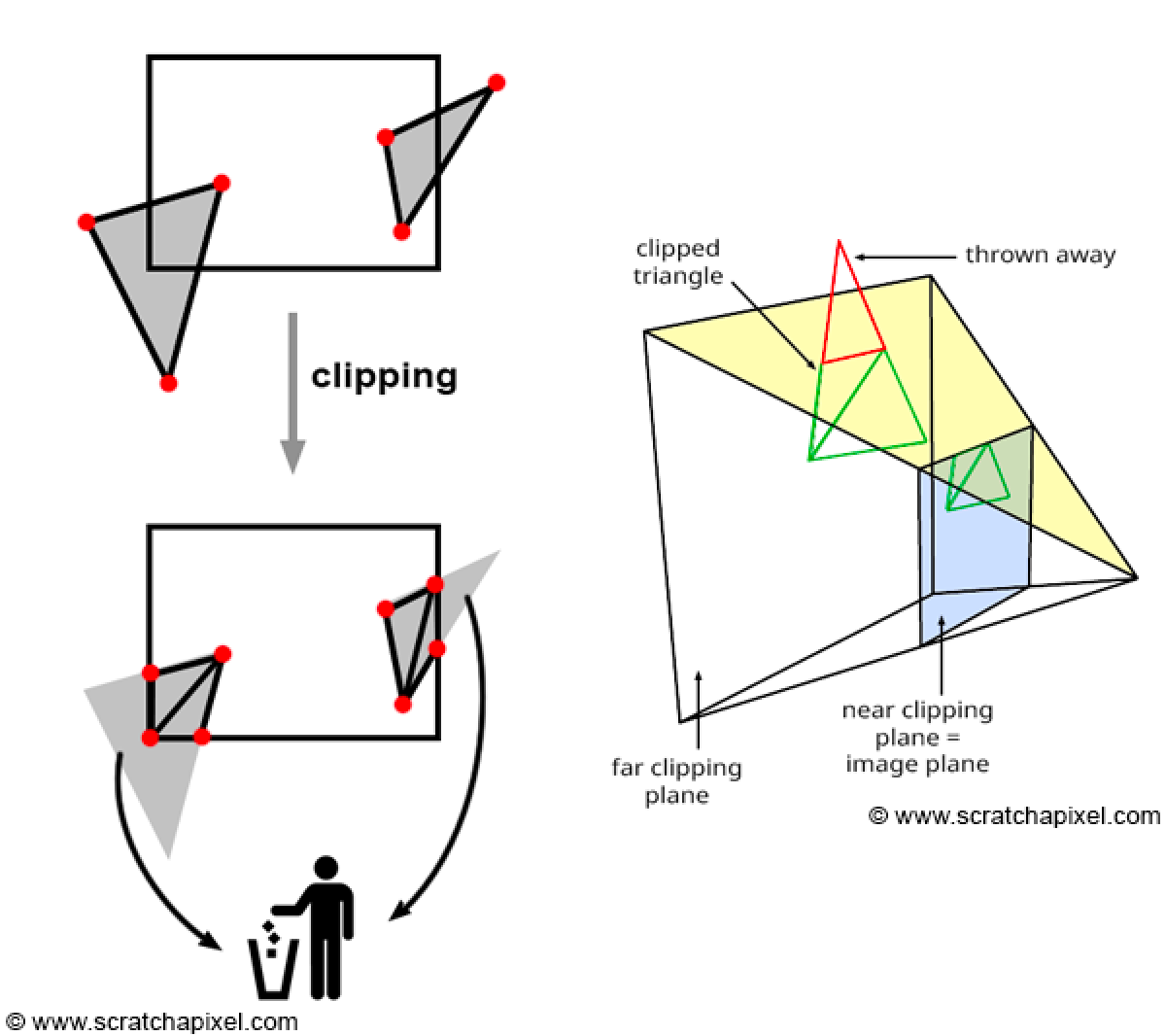
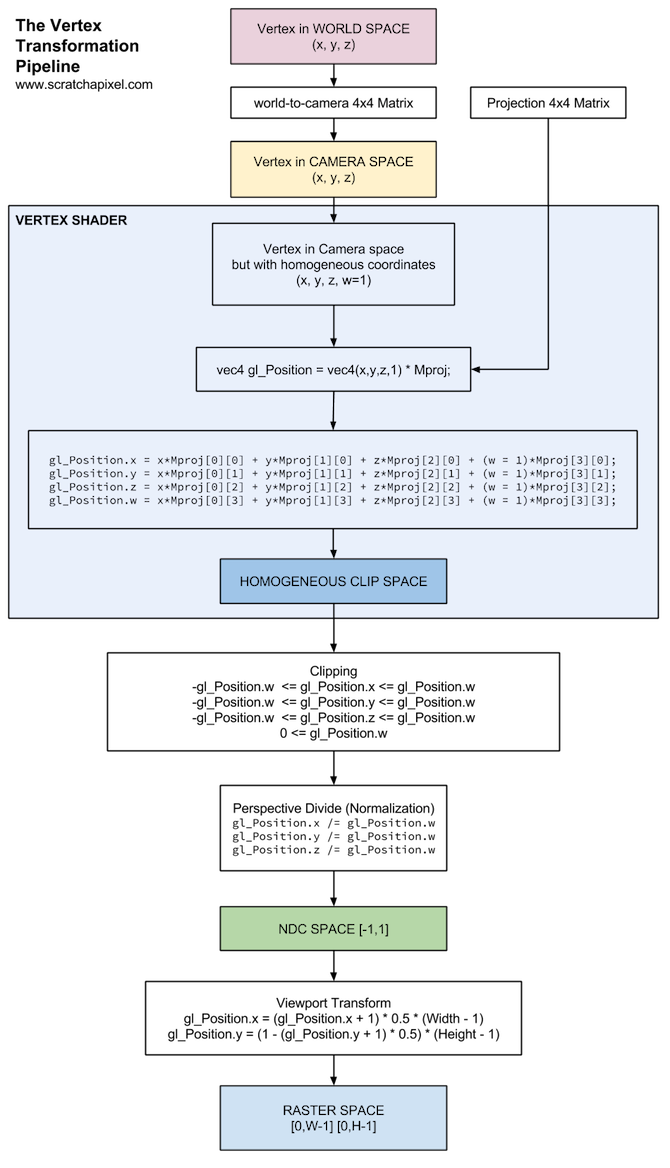
在图形学渲染管线中，一个顶点坐标，大概要经历局部坐标系、世界坐标系、相机坐标系、裁剪坐标系，最后到窗口坐标系，显示在屏幕上。

在这些过程中，从一个坐标系到另一个坐标系，都需要进行一定的变换。下面，将介绍每次变换的方式。

局部空间->世界空间

这一变换过程，主要是将模型放置在世界空间中，进行一定的缩放、旋转或平移。这一步比较简单，只要将相应的矩阵作用到模型的局部空间坐标即可。

比如，对模型缩放$(S_x, S_y, S_z)$ ，然后绕Z轴旋转$\theta$度，再进行$(T_x,T_y,T_z)$的平移。注意，这里的变换顺序是不能变的，即要先进行缩放，再进行旋转，最后进行平移。据此，我们可以构建模型变换矩阵。

$$ M_{\text {model }}=\left[\begin{array}{cccc} 1 & 0 & 0 & T_x \ 0 & 1 & 0 & T_y \ 0 & 0 & 1 & T_z \ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} \cos \theta & -\sin \theta & 0 & 0 \ \sin \theta & \cos \theta & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} S_x & 0 & 0 & 0 \ 0 & S_y & 0 & 0 \ 0 & 0 & S_z & 0 \ 0 & 0 & 0 & 1 \end{array}\right] $$

世界空间->相机空间

首先定义一下相机：

• 坐标为$\vec{e}$
• 观察方向
• 向上方向