B-Tree

为了描述B-Tree，首先定义一条数据记录为一个二元组[key, data]，key为记录的键值，对于不同数据记录，key是互不相同的；data为数据记录除key外的数据。

那么B-Tree是满足下列条件的数据结构：

• 一个节点中的key从左到右非递减排列。所有节点组成树结构。每个指针要么为null，要么指向另外一个节点。
• 每个叶节点最少包含一个key和两个指针，最多包含2d-1个key和2d个指针。key和指针互相间隔，节点两端是指针。
• 叶子节点的指针均为null，所有子叶节点具有相同的深度，等于树高h。

B-Tree还中的父子节点还满足以下排序规则：

• 如果某个指针在节点node最左边且不为null，则其指向节点的所有key小于v(key1)，其中v(key1)为node的第一个key的值。
• 如果某个指针在节点node最右边且不为null，则其指向节点的所有key大于v(keym)，其中v(keym)为node的最后一个key的值。
• 如果某个指针在节点node的左右相邻key分别是keyi和keyi+1且不为null，则其指向节点的所有key小于v(keyi+1)且大于v(keyi)。

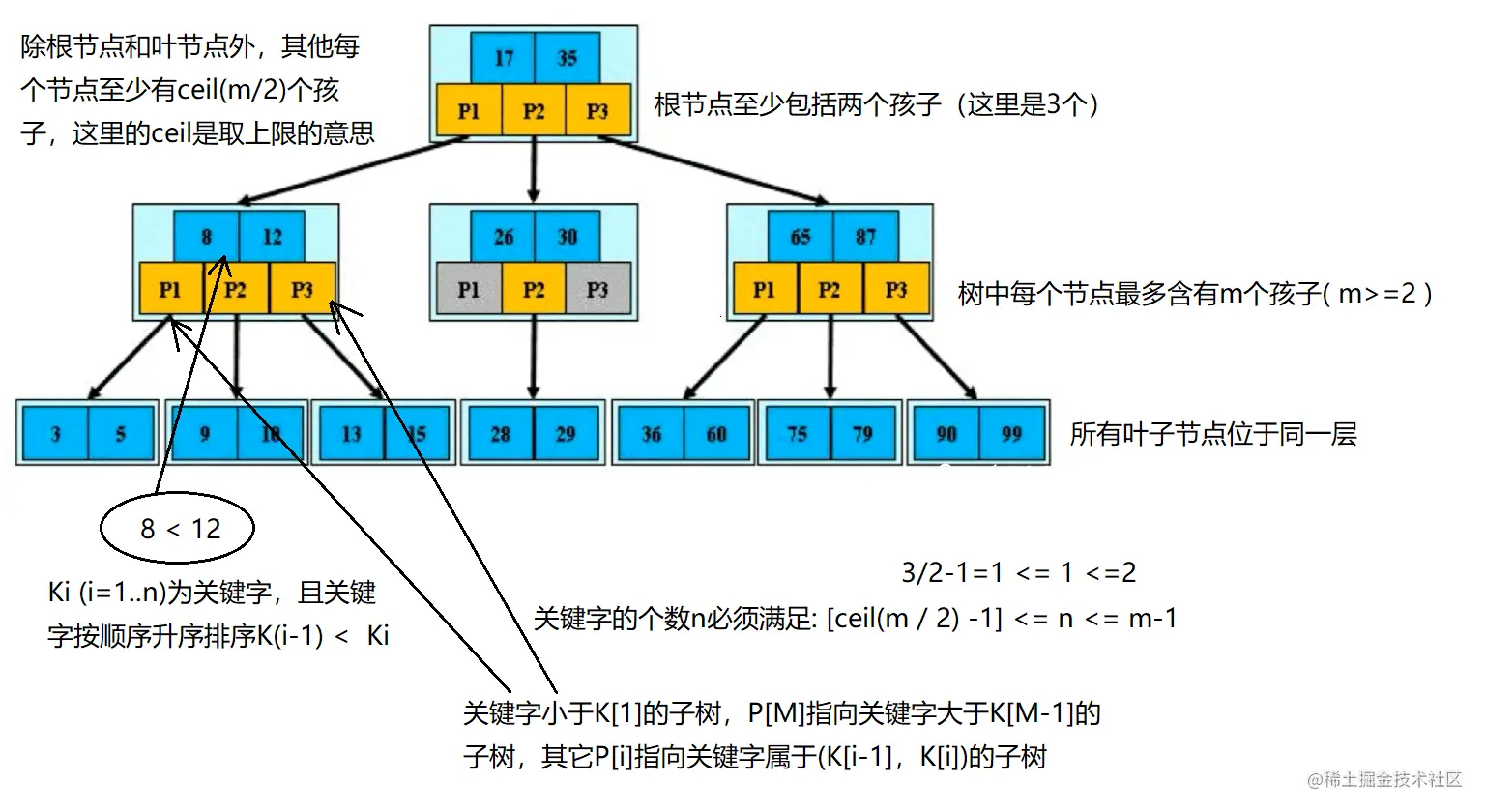
由于B-Tree的特性，在B-Tree中按key检索数据的算法非常直观：首先从根节点进行二分查找，如果找到则返回对应节点的data，否则对相应区间的指针指向的节点递归进行查找，直到找到节点或找到null指针，前者查找成功，后者查找失败。B-Tree上查找算法的伪代码如下：

BTree_Search(node,key) {
    if(node == null) returnnull;
    foreach(node.key){
        if(node.key[i]== key) return node.data[i];
        if(node.key[i]> key) return BTree_Search(point[i]->node, key);
    }
    return BTree_Search(point[i+1]->node, key);
}
data =BTree_Search(root, my_key);

关于B-Tree有一系列有趣的性质，例如一个度为d的B-Tree，设其索引N个key，则其树高h的上限为logd((N+1)/2)，检索一个key，其查找节点个数的渐进复杂度为O(logdN)。从这点可以看出，B-Tree是一个非常有效率的索引数据结构。