深度优先搜索
深度优先搜索
图的深度优先搜索（Depth First Search
显然，深度优先搜索是一个递归的过程。
int book[100], sum, n, e[100][100];
void dfs(int cur){ // cur 当前所在顶点编号
sum++;
if(sum == n) return; // 所有顶点都已经访问过就直接退出
for(int i=0; i<n; i++){
if(e[cur][i] == 1 && book[i] == 0){
book[i] = 1; // 标记顶点i已经访问过
dfs(i); // 从顶点i再出发继续遍历
}
}
return;
}
无向图的深度优先搜索
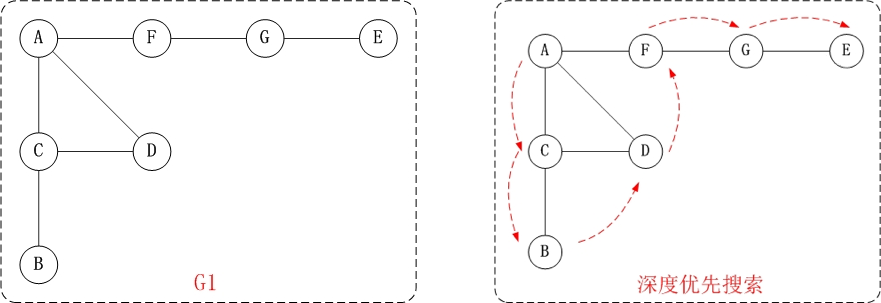
- 第
1 步：访问A 。 - 第
2 步：访问(A 的邻接点)C 。在第1 步访问A 之后，接下来应该访问的是A 的邻接点，即"C,D,F" 中的一个。但在本文的实现中，顶点ABCDEFG 是按照顺序存储，C 在"D 和F" 的前面，因此，先访问C 。 - 第
3 步：访问(C 的邻接点)B 。在第2 步访问C 之后，接下来应该访问C 的邻接点，即"B 和D" 中一个(A 已经被访问过，就不算在内) 。而由于B 在D 之前，先访问B 。 - 第
4 步：访问(C 的邻接点)D 。在第3 步访问了C 的邻接点B 之后，B 没有未被访问的邻接点；因此，返回到访问C 的另一个邻接点D 。 - 第
5 步：访问(A 的邻接点)F 。前面已经访问了A ，并且访问完了"A 的邻接点B 的所有邻接点( 包括递归的邻接点在内)" ；因此，此时返回到访问A 的另一个邻接点F 。 - 第
6 步：访问(F 的邻接点)G 。 - 第
7 步：访问(G 的邻接点)E 。
因此访问顺序是：A -> C -> B -> D -> F -> G -> E
有向图的深度优先搜索
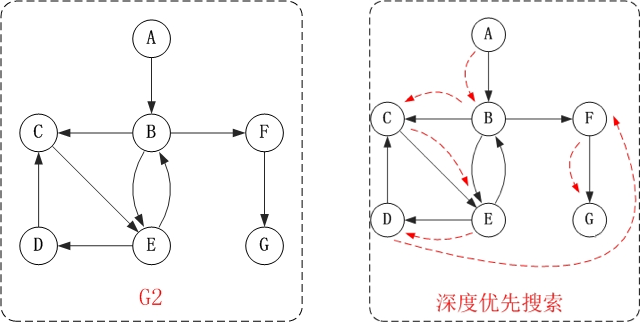
- 第
1 步：访问A 。 - 第
2 步：访问B 。在访问了A 之后，接下来应该访问的是A 的出边的另一个顶点，即顶点B 。 - 第
3 步：访问C 。在访问了B 之后，接下来应该访问的是B 的出边的另一个顶点，即顶点C,E,F 。在本文实现的图中，顶点ABCDEFG 按照顺序存储，因此先访问C 。 - 第
4 步：访问E 。接下来访问C 的出边的另一个顶点，即顶点E 。 - 第
5 步：访问D 。接下来访问E 的出边的另一个顶点，即顶点B,D 。顶点B 已经被访问过，因此访问顶点D 。 - 第
6 步：访问F 。接下应该回溯" 访问A 的出边的另一个顶点F" 。 - 第
7 步：访问G 。
因此访问顺序是：A -> B -> C -> E -> D -> F -> G
深度优先遍历
图的深度优先遍历基于深度优先搜索
下图（a）给出了深度优先搜索的示例。由于该图是连通的，所以从顶点
从指定的结点
（1）访问结点
深度优先遍历的主要思想是：首先以一个未被访问过的顶点作为起始顶点，沿着当前顶点的边走到未被访问过的顶点；当没有未被访问过的顶点时，回到上一个顶点，继续试探访问别的顶点，直到所有的顶点都被访问过。显然，深度优先遍历是沿着图的某一条分支遍历直到末端，然后回溯，再沿着另一条继续遍历，直到所有的顶点都被访问过为止。
算法实现
// 深度优先遍历的算法
template<class vertexType, class arcType>void Graph <vertexType, arcType> ::
DFTraverse ( void visit( vertexType v )) {
int i, n = NumberOfVertexes() ;//取图的顶点个数
int * visited = new int [n]; //定义访问标记数组 visited
for ( i = 0; i < n; i++ )
visited [i] = 0; //访问标记数组 visited 初始化
for ( i = 0; i < n; i++ ) //对图中的每一个顶点进行判断
if (!visited [i]) DFS (v, visited, visit );
delete [ ] visited; //释放 visited
}
// 深度优先搜索
template<class vertexType, class arcType>void
Graph<vertexType, arcType> ::
DFS ( const int v, int visited [ ], void visit( vertexType v )) {
visit( GetValue (v)); //访问顶点 v
visited[v] = 1; //顶点v 作访问标记
int w = GetFirstNeighbor (v);
while ( w != -1 ) { //若顶点 w 存在
if ( !visited[w] ) DFS ( w, visited );
w = GetNextNeighbor ( v, w );
} //重复检测 v 的所有邻接顶点
}
最短路径的实现：
int min = 999999999, n, book[100], e[100][100];
void dfs(int cur, int dis){
if(dis > min) return;
if(cur == n){ // 判断是否到达目标城市
if(dis < min) min = dis; // 更新最小值
return；
}
for(int i=0; i<n; i++){
if(e[cur][i] != 99999999 && book[i] == 0){
book[i] = 1;
dfs(i,dis+e[cur][i]);
book[i] = 0;
}
}
return;
}